题目大意:
将箱子放进仓库1
Given two arrays of positive integers boxes and warehouse representing the heights of some boxes of unit width, and the heights of n rooms in a warehouse, respectively. The warehouse’s rooms are labeled from 0 to n - 1 from left to right where warehouse[i] (0-indexed) is the height of the ith room.
Boxes are put into the warehouse by the following rules:
- Boxes can’t be piled up.
- You can rearrange the order of the boxes.
- Boxes can only be pushed into the warehouse from left to right only.
- If the height of some room in the warehouse is less than the height of a box, then the box will be stopped before that room, so are the boxes behind it.
Return the maximum number of boxes you can put into the warehouse.
示例1:
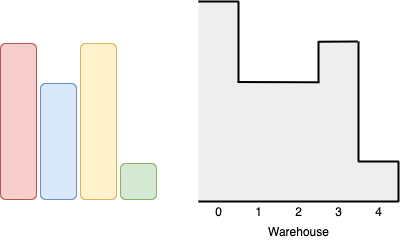
输入: boxes = [4,3,4,1], warehouse = [5,3,3,4,1] 输出: 3 解释:We can first put the box of height 1 in room 4. Then we can put the box of height 3 in either of the 3 rooms 1, 2, or 3. Lastly, we can put one box of height 4 in room 0. There is no way we can fit all 4 boxes in the warehouse.
示例2:
输入: boxes = [1,2,2,3,4], warehouse = [3,4,1,2] 输出: 3 解释:Notice that it's not possible to put the box of height 4 into the warehouse since it cannot pass the first room of height 3. Also, for the last two rooms, 2 and 3, only boxes of height 1 can fit. We can fit 3 boxes maximum as shown above. The yellow box can also be put in room 2 instead. Swapping the orange and green boxes is also valid, or swapping one of them with the red box.
Example 3:
Input: boxes = [1,2,3], warehouse = [1,2,3,4] Output: 1 Explanation: Since the first room in the warehouse is of height 1, we can only put boxes of height 1.
Example 4:
Input: boxes = [4,5,6], warehouse = [3,3,3,3,3] Output: 0
Constraints:
n == warehouse.length1 <= boxes.length, warehouse.length <= 10^51 <= boxes[i], warehouse[i] <= 10^9
如果想查看本题目是哪家公司的面试题,请参考以下免费链接: https://leetcode.jp/problemdetail.php?id=1564
解题思路分析:
这道题是向仓库内放箱子,题目给出的仓库很奇怪,它的屋顶高度是错落无序的。由于我们只能从仓库左边向内放入,因此,如果想放入更多的箱子,应该使得先进入的箱子应该尽量放到仓库的靠右的位置。而一个箱子能否放到某个位置i上,取决于仓库的最左边(下标0)到当前位置下标i的区间内,是否高度都大于等于当前箱子的高度,如果是,才能保证箱子能顺利从仓库的左边入口移动到下标i处。解题时:
- 我们需要先对数据进行预处理,即算出仓库的每一个位置上到入口间的最小高度,即leftMinHeight[i]表示下标0到i间的最小高度。计算这个高度很简单,我们使用一个循环,从仓库下标0循环至末尾。下标0处,leftMinHeight[0]等于仓库位置0处的高度warehouse[0],而其他位置leftMinHeight[i]则等于: min(warehouse[i],leftMinHeight[i-1])
- 接下来我们对箱子按照高度进行排序
- 将当前箱子尽量向仓库的右边放。即使用双指针,初始时,箱子指针指向下标0(高度最小的箱子),仓库指针指向仓库最右端。如果当前箱子的高度小于等于leftMinHeight[i],即,当前箱子可以从入口移动到仓库当前位置,此时,返回结果加一,同时箱子指针向右移动一位,仓库指针向左移动一位。反之,代表当前箱子无法顺利移动到仓库当前位置,那么,我们只能将仓库位置向左移动一位。重复上述操作,直到仓库位置小于0,或者箱子下标大于等于箱子个数时为止。
实现代码(Java版本):
public int maxBoxesInWarehouse(int[] boxes, int[] warehouse) {
int[] leftMinHeight = new int[warehouse.length]; // 统计仓库当前位置到入口间的最小高度
for(int i=0;i<warehouse.length;i++){ // 循环仓库每个位置
if(i==0) leftMinHeight[i]=warehouse[i]; // 如果下标为0,最小高度为当前高度
// 否则最小高度为当前高度与前移最小高度的最小值
else leftMinHeight[i]=Math.min(leftMinHeight[i-1],warehouse[i]);
}
Arrays.sort(boxes); // 箱子按照高度排序
int res=0; // 返回结果
int boxIndex=0; // 箱子下标
int houseIndex=leftMinHeight.length-1; // 仓库下标
while(boxIndex<boxes.length&&houseIndex>=0){
// 如果箱子可以移动到当前位置
if(boxes[boxIndex]<=leftMinHeight[houseIndex]){
res++; // 返回结果加一
boxIndex++; // 箱子下标加一(继续放下一个箱子)
houseIndex--; // 仓库下标减一(继续从当前位置左边开始尝试放箱子)
}else{ // 无法移动到当前位置
houseIndex--; // 仓库下标减一(继续从当前位置左边开始尝试放箱子)
}
}
return res;
}本题解法执行时间为16ms。
Runtime: 16 ms, faster than 100.00% of Java online submissions for Put Boxes Into the Warehouse I.
Memory Usage: 52.7 MB, less than 100.00% of Java online submissions for Put Boxes Into the Warehouse I.
实现代码(Kotlin版本):
fun maxBoxesInWarehouse(boxes: IntArray, warehouse: IntArray): Int {
var leftMinHeight = mutableListOf<Int>()
for(i in 0..(warehouse.size-1)){
leftMinHeight.add(
if(i==0)
warehouse[0]
else
Math.min(warehouse[i],leftMinHeight[i-1]))
}
Arrays.sort(boxes);
var res = 0
var indexBox = 0
var indexHouse = warehouse.size-1
while(indexHouse>=0&&indexBox<leftMinHeight.size){
if(boxes[indexBox]<=leftMinHeight[indexHouse]){
res++
indexBox++
indexHouse--
}else{
indexHouse--
}
}
return res;
}本网站文章均为原创内容,并可随意转载,但请标明本文链接如有任何疑问可在文章底部留言。为了防止恶意评论,本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言,并会在第一时间对您的留言进行回复!欢迎交流!
本文链接: https://leetcode.jp/leetcode-1564-put-boxes-into-the-warehouse-i-解题思路分析/
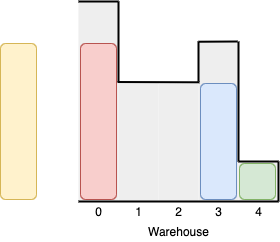 We can first put the box of height 1 in room 4. Then we can put the box of height 3 in either of the 3 rooms 1, 2, or 3. Lastly, we can put one box of height 4 in room 0. There is no way we can fit all 4 boxes in the warehouse.
We can first put the box of height 1 in room 4. Then we can put the box of height 3 in either of the 3 rooms 1, 2, or 3. Lastly, we can put one box of height 4 in room 0. There is no way we can fit all 4 boxes in the warehouse.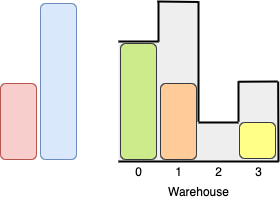 Notice that it's not possible to put the box of height 4 into the warehouse since it cannot pass the first room of height 3. Also, for the last two rooms, 2 and 3, only boxes of height 1 can fit. We can fit 3 boxes maximum as shown above. The yellow box can also be put in room 2 instead. Swapping the orange and green boxes is also valid, or swapping one of them with the red box.
Notice that it's not possible to put the box of height 4 into the warehouse since it cannot pass the first room of height 3. Also, for the last two rooms, 2 and 3, only boxes of height 1 can fit. We can fit 3 boxes maximum as shown above. The yellow box can also be put in room 2 instead. Swapping the orange and green boxes is also valid, or swapping one of them with the red box.