题目大意:
安排邮筒
给你一个房屋数组houses 和一个整数 k ,其中 houses[i] 是第 i 栋房子在一条街上的位置,现需要在这条街上安排 k 个邮筒。
请你返回每栋房子与离它最近的邮筒之间的距离的 最小 总和。
答案保证在 32 位有符号整数范围以内。
示例 1:
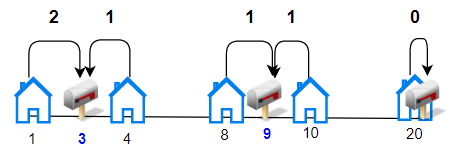
输入:houses = [1,4,8,10,20], k = 3 输出:5 解释:将邮筒分别安放在位置 3, 9 和 20 处。 每个房子到最近邮筒的距离和为 |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5 。
示例 2:
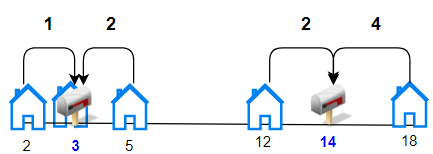
输入:houses = [2,3,5,12,18], k = 2 输出:9 解释:将邮筒分别安放在位置 3 和 14 处。 每个房子到最近邮筒距离和为 |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9 。
示例 3:
输入:houses = [7,4,6,1], k = 1 输出:8
示例 4:
输入:houses = [3,6,14,10], k = 4 输出:0
提示:
- n == houses.length
- 1 <= n <= 100
- 1 <= houses[i] <= 10^4
- 1 <= k <= n
- 数组 houses 中的整数互不相同。
如果想查看本题目是哪家公司的面试题,请参考以下免费链接: https://leetcode.jp/problemdetail.php?id=1478
解题思路分析:
对于如何安排邮箱位置,看到很多文章说应放在中位数的位置上,比如一共有1,2,3,4这4间房屋,不论房屋间的距离是多少,如果只有一个邮箱的话,放在房间2处(3也可以)最为合理。这个说法虽然正确,但实际上并不恰当。我们简单的讨论一下这个问题:
- 当只有1栋房屋,1个邮箱时,显然将邮箱放在房屋处最为合理,这时邮箱与房屋的距离为0。
- 当有2栋房屋,1个邮箱时,比如房屋1在坐标0处,房屋2在坐标10处,此时如果将邮箱放在坐标0的话,它与两栋房屋的距离和为10。放在坐标10的情况下距离和也为10。另外我们可以看出,不论邮箱放在两栋房屋之间的任意位置上,它与房屋的距离和都是10。因此通过此例可得出,中位数的说法虽然正确,但并不全面,不过这不影响本题解题,对于本题,我们统一将邮箱安排在房屋位置上是为了方便计算,因此才得出中位数的说法(本例房屋1和2都可以看做是中位数)。
- 当有3栋房屋,1个邮箱时,此时通过上面的例子可知,对于两侧的房子,将邮筒放在他们之间的任何位置对于结果没有任何影响,距离和都是两栋房子间的距离。但邮箱的位置会对中间的房子产生影响,因此,将其放置在中间房子的坐标上最为合理,这样邮箱与中间房屋的距离为0,可使得全局总距离最小。而中间的房屋正是3个房屋的中位数。
- 当有4栋房屋,1个邮箱时,与上例同理,对于两侧的房子,将邮筒放在他们之间的任何位置对于结果没有任何影响,因此邮箱可以考虑放在中间两个房屋的任何一个位置上。另外对于中间两个房屋,不论邮箱放置在其任何一个位置上,对于总距离都不会产生影响(这相当于第2条)。
因此我们可以得出结论,当有N栋房屋,1个邮箱时,我们将邮箱放在房屋下标的中位数上最为合理。那么,如果有多个邮箱时该怎么办?其实也不难,本题最终可以理解为,我们将一个房屋数组分割为K个子数组(k为邮筒个数),每一个子数组中放置一个邮筒,求最优分割方式。这就变为了经典的动态规划DP问题,对于DP问题我习惯采用递归加记忆数组的方式,本题我们也采用递归方式讲解。
首先建立一个递归函数,参数为当前子区间开始位置index,以及剩余未分配邮筒个数k。起始时,子区间开始位置为下标0,邮筒个数为题目给定的整数k。递归时,当前子区间的开始坐标是参数index,结束坐标范围理论上可以是当前index到数组末尾为止,不过这里有一处可以优化,即要保证剩下的k-1个邮筒都能分配出去的话,还需要至少k-1个子区间,也就是说除了当前子区间外还至少需要k-1个房屋,因此当前子区间的结束坐标范围应该是当前index到length-k为止。我们从index循环至length-k,分别作为当前子区间的结束位置end。并通过中位数方式求出当前子区间[index, end]放置邮筒后的距离和(后文会给出方法)。然后将end加一作为下一个子区间的开始位置,同时k值减去一作为参数传入递归子问题中继续求解。递归函数的返回值加上当前子区间的距离和即是选择当前子区间范围后的一个结果sum。循环完所有当前子区间的结束位置end之后,所有sum中的最小值即是最优方案,也是本层递归的返回值。
接下来再为递归加上一个记忆数组。记忆数组相当于动态规划中使用到的DP数组。由于递归函数中存在2个变量,因此我们需要使用一个2维数组来描述该递归函数,并记录它的返回值。
最后,上文中提到需要求解子区间内放置一个邮筒后所有房屋与邮筒的距离和。这个问题没有太好的方式,只能暴力累加每个房屋与中位数房屋所在位置的距离。为了提高效率,我们可以事先计算好所有区间(排列组合)内放置一个邮筒时的距离和,方便递归中使用,也避免重复运算。这里可能有人会提出质疑,既然递归方法中已经使用了记忆数组,目的就是防止重复计算,这里为什么还担心重复计算距离和呢?原因很简单,记忆数组是二维数组,即在两个条件都满足的情况下才会使用记忆数组中的数据,比如我们计算过以下标5作为子区间起点,并且当前还剩2个油桶的递归函数返回值为x,即memo[5][2]=x,再次遇到相同问题时我们可以直接返回x。但是遇到memo[5][1]或者memo[5][3]时,我们尚未做出过计算,同样还会进入到递归函数内部,如果没有事前计算好下标5到end(end取值范围是5到length-k)的距离和的话,还要重复计算一遍。
对于上述问题,还有一个更好的优化方式即再建立一个保存距离和的记忆数组,计算一个距离和记录一个,方便下次使用。
实现代码:
int[][] memo; // 递归记忆数组
int[][] memoDis; // 距离和记忆数组
public int minDistance(int[] houses, int k) {
Arrays.sort(houses); // 排序房屋位置
int n=houses.length; // 房屋个数
memo=new int[n+1][n]; // 初始化记忆数组
memoDis=new int[n][n]; // 初始化记忆数组
return help(houses,k,0); // 递归求解
}
// houses:房屋数组
// k:当前尚未分配邮筒个数
// index:当前子区间起始位置
// 从当前index开始到数组结束,安排k个邮筒后距离和最小值
int help(int[] houses, int k, int index){
// 如果数组越界,返回0
if(index==houses.length) return 0;
// 还剩下1个邮筒,安排在数组剩余区间的中位数上即可,求距离和并返回
if(k==1) return getDis(houses,index,houses.length-1);
// 如果记忆数组中存在当前解,直接返回记忆数组中的值
if(memo[k][index]>0) return memo[k][index];
// 当前最优解
int min=Integer.MAX_VALUE;
// 循环当前区间的结束坐标
for(int i=index;i<=houses.length-k;i++){
// 以当前区间结束坐标加一为下一个区间的起始坐标,递归至子问题
int res=help(houses,k-1,i+1);
// 子问题解加上当前区间的距离和为当前的一个解,用该解更新全局最优解
min=Math.min(getDis(houses,index,i)+res,min);
}
// 将当前最优解计入记忆数组
memo[k][index]=min;
return min;
}
// 求区间start到end间放置邮筒后的距离和
int getDis(int[] houses, int start, int end){
// 如果记忆数组中存在当前解,直接返回
if(memoDis[start][end]>0) return memoDis[start][end];
// 计算下标中位数
int mid=(start+end)/2;
// 距离和
int sum=0;
for(int h=start;h<=end;h++){
// 累加每一个房子距离中位数房子的距离
sum+=Math.abs(houses[h]-houses[mid]);
}
// 将结果保存至记忆数组
memoDis[start][end]=sum;
return sum;
}本题解法执行时间为9ms。
Runtime: 9 ms, faster than 89.16% of Java online submissions for Allocate Mailboxes.
Memory Usage: 38.8 MB, less than 100.00% of Java online submissions for Allocate Mailboxes.
本网站文章均为原创内容,并可随意转载,但请标明本文链接如有任何疑问可在文章底部留言。为了防止恶意评论,本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言,并会在第一时间对您的留言进行回复!欢迎交流!
本文链接: https://leetcode.jp/leetcode-1478-allocate-mailboxes-解题思路分析/