题目大意:
切割后面积最大的蛋糕
矩形蛋糕的高度为 h 且宽度为 w,给你两个整数数组 horizontalCuts 和 verticalCuts,其中 horizontalCuts[i] 是从矩形蛋糕顶部到第 i 个水平切口的距离,类似地, verticalCuts[j] 是从矩形蛋糕的左侧到第 j 个竖直切口的距离。
请你按数组 horizontalCuts 和 verticalCuts 中提供的水平和竖直位置切割后,请你找出 面积最大 的那份蛋糕,并返回其 面积 。由于答案可能是一个很大的数字,因此需要将结果对 10^9 + 7 取余后返回。
示例 1:
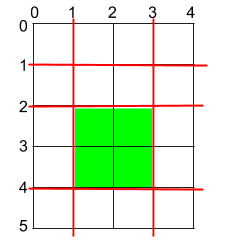
输入:h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3] 输出:4 解释:上图所示的矩阵蛋糕中,红色线表示水平和竖直方向上的切口。切割蛋糕后,绿色的那份蛋糕面积最大。
示例 2:
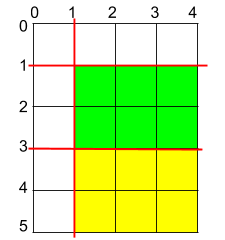
输入:h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1] 输出:6 解释:上图所示的矩阵蛋糕中,红色线表示水平和竖直方向上的切口。切割蛋糕后,绿色和黄色的两份蛋糕面积最大。
示例 3:
输入:h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3] 输出:9
提示:
- 2 <= h, w <= 10^9
- 1 <= horizontalCuts.length < min(h, 10^5)
- 1 <= verticalCuts.length < min(w, 10^5)
- 1 <= horizontalCuts[i] < h
- 1 <= verticalCuts[i] < w
- 题目数据保证 horizontalCuts 中的所有元素各不相同
- 题目数据保证 verticalCuts 中的所有元素各不相同
如果想查看本题目是哪家公司的面试题,请参考以下免费链接: https://leetcode.jp/problemdetail.php?id=1465
解题思路分析:
本题最笨的方法即是遍历出每一个格子的面积然后取最大值。不过数据规模并不允许这个级别的时间复杂度。其实,仔细想想,本题并没有那么复杂,我们只要找出最大的横格,与最大的纵格,他们相交处的面积一定是最大的,即返回结果。
另外需要注意一点,遍历最大距离时,别忘记边界,如左边界与第1条纵切,再比如下边界与最后一条横切。
实现代码:
public int maxArea(int h, int w, int[] horizontalCuts, int[] verticalCuts) {
Arrays.sort(horizontalCuts); // 排序所有横切
Arrays.sort(verticalCuts); // 排序所有纵切
// 最大横切间距(默认为最大高度到最后一刀横切间距离)
long maxH=h-horizontalCuts[horizontalCuts.length-1];
// 最大纵切间距(默认为最大宽度到最后一刀纵切间距离)
long maxW=w-verticalCuts[verticalCuts.length-1];
// 循环每一纵切,找到最大纵切间距离
for(int i=0;i<verticalCuts.length;i++){
int width=verticalCuts[i]-(i==0?0:verticalCuts[i-1]);
maxW=Math.max(maxW,width);
}
// 循环每一横切,找到最大横切间距离
for(int i=0;i<horizontalCuts.length;i++){
int height=horizontalCuts[i]-(i==0?0:horizontalCuts[i-1]);
maxH=Math.max(maxH,height);
}
// 两者乘积为最大面积
long area=maxW*maxH;
return (int)(area%1000000007);
}本题解法执行时间为14ms。
Runtime: 14 ms, faster than 79.02% of Java online submissions for Maximum Area of a Piece of Cake After Horizontal and Vertical Cuts.
Memory Usage: 49.4 MB, less than 100.00% of Java online submissions for Maximum Area of a Piece of Cake After Horizontal and Vertical Cuts.
本网站文章均为原创内容,并可随意转载,但请标明本文链接如有任何疑问可在文章底部留言。为了防止恶意评论,本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言,并会在第一时间对您的留言进行回复!欢迎交流!
本文链接: https://leetcode.jp/leetcode-1465-maximum-area-of-a-piece-of-cake-after-horizontal-and-vertical-cuts-解题思路分析/