题目大意:
切披萨的方案数
给你一个 rows x cols 大小的矩形披萨和一个整数 k ,矩形包含两种字符: ‘A’ (表示苹果)和 ‘.’ (表示空白格子)。你需要切披萨 k-1 次,得到 k 块披萨并送给别人。
切披萨的每一刀,先要选择是向垂直还是水平方向切,再在矩形的边界上选一个切的位置,将披萨一分为二。如果垂直地切披萨,那么需要把左边的部分送给一个人,如果水平地切,那么需要把上面的部分送给一个人。在切完最后一刀后,需要把剩下来的一块送给最后一个人。
请你返回确保每一块披萨包含 至少 一个苹果的切披萨方案数。由于答案可能是个很大的数字,请你返回它对 10^9 + 7 取余的结果。
示例 1:
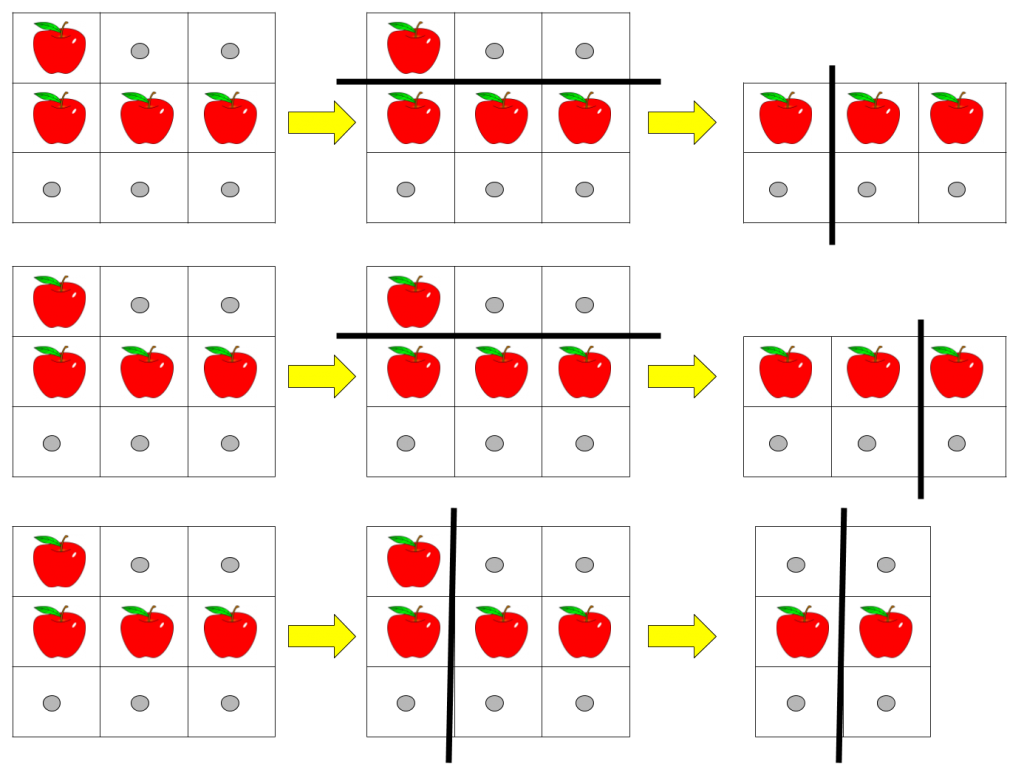
输入:pizza = ["A..","AAA","..."], k = 3 输出:3 解释:上图展示了三种切披萨的方案。注意每一块披萨都至少包含一个苹果。
示例 2:
输入:pizza = ["A..","AA.","..."], k = 3 输出:1
示例 3:
输入:pizza = ["A..","A..","..."], k = 1 输出:1
提示:
- 1 <= rows, cols <= 50
- rows == pizza.length
- cols == pizza[i].length
- 1 <= k <= 10
- pizza 只包含字符 ‘A’ 和 ‘.’ 。
如果想查看本题目是哪家公司的面试题,请参考以下免费链接: https://leetcode.jp/problemdetail.php?id=1444
解题思路分析:
我们之前多次强调过,看到答案会很大的题目(比如需要对 10^9 + 7 取余),一般来说都要采用动态规划(DP)的方式来思考。对于dp题目,我习惯使用递归加记忆数组的方式来解题。本题也不例外。
递归函数中,我们定义3个重要参数,分别代表披萨当前的开始行与列,以及剩余的刀数。递归中对于当前披萨,我们可以横切或者纵切将其分割成2部分。我们分别尝试每种切割方式,分割后,上半部分或者左半部分是当前要分给他人的一部分,因此我们需要判断该部分内是否含有苹果,如果没有的话,说明当前分割不合理,应继续循环至下一种分割方式。反之如果含有苹果的话,我们可以将剩下的部分(右边或者下边)交给子问题(递归)去解决。循环中所有子问题的返回结果之和,为当前递归的返回结果。递归的结束条件是当k等于1(切完k-1刀)时,查看当前剩下的披萨中是否含有苹果,如果含有的话返回1,反之返回0。
最后再来考虑记忆数组的问题。记忆数组的定义方式是查看递归函数的参数中含有几个可变的变量。本题中,当前列,当前行,以及剩余刀数这三个参数是不断变化的,因此我们需要使用一个三维数组来定义该记忆数组。
实现代码:
Integer memo[][][]; // 记忆数组
public int ways(String[] pizza, int k) {
char[][] arr = new char[pizza.length][pizza[0].length()];
// 为了方便,先将pizza转化为二维字符数组
for(int i=0;i<pizza.length;i++){
String piz=pizza[i];
arr[i] = piz.toCharArray();
}
// 初始化记忆数组
memo=new Integer[arr.length][arr[0].length][k+1];
// 递归求解
return help(arr, 0,0,k);
}
// arr:披萨数组
// row:当前开始行
// col:当前开始列
// k:剩余刀数
int help(char[][] arr, int row, int col, int k){
// 切完所有刀后
if(k==1){
// 如果当前剩余披萨中含有苹果,返回true,反之返回false
return hasApple(arr, row, arr.length-1, col, arr[0].length-1)?1:0;
}
// 如果记忆数组中存在当前解,返回记忆数组中的值
if(memo[row][col][k]!=null) return memo[row][col][k];
// 当前递归返回结果
long res=0;
// 分别循环横向每一种切法(上半部分存在1行,2行,3行。。。)
for(int i=row;i<arr.length-1;i++){
// 如果上半部分中有苹果
if(hasApple(arr,row,i,col, arr[0].length-1)){
// 将下半部分剩余披萨递归至子问题
// 子问题的返回结果累加至当前返回结果
res+=help(arr,i+1,col,k-1);
}
}
// 纵切同理
for(int i=col;i<arr[0].length-1;i++){
if(hasApple(arr,row,arr.length-1,col,i)){
res+=help(arr,row,i+1,k-1);
}
}
// 将返回结果取余后转为int型
int count=(int)(res%1000000007);
// 保存至记忆数组
memo[row][col][k]=count;
return count;
}
// 查看当前区域是否含有苹果
boolean hasApple(char[][] arr, int rowT,int rowB, int colL, int colR){
for(int r=rowT;r<=rowB;r++){
for(int c=colL;c<=colR;c++){
if(arr[r][c]=='A') return true;
}
}
return false;
}本题解法执行时间为8ms。
Runtime: 8 ms, faster than 100.00% of Java online submissions for Number of Ways of Cutting a Pizza.
Memory Usage: 37.3 MB, less than 100.00% of Java online submissions for Number of Ways of Cutting a Pizza.
本网站文章均为原创内容,并可随意转载,但请标明本文链接如有任何疑问可在文章底部留言。为了防止恶意评论,本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言,并会在第一时间对您的留言进行回复!欢迎交流!
本文链接: https://leetcode.jp/leetcode-1444-number-of-ways-of-cutting-a-pizza-解题思路分析/