LEETCODE 1168. Optimize Water Distribution in a Village 解题思路分析

题目大意：

水资源分配优化

村庄内有n户人家，我们可以通过挖井或者建造水管向每家供水。

对于每户人家i，我们可以通过花费 wells[i] 直接在其房内挖水井，或者通过水管连接到其他的水井。每两户住户间铺设水管的费用通过 pipes 数组表示。 pipes[i] = [house1, house2, cost] 表示住户1到住户2间铺设水管的费用为cost。

请求出所有住户都能通水的最小花费。

示例1：

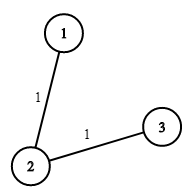
输入: n = 3, wells = [1,2,2], pipes = [[1,2,1],[2,3,1]]
输出: 3
解释: 
The image shows the costs of connecting houses using pipes.
The best strategy is to build a well in the first house with cost 1 and connect the other houses to it with cost 2 so the total cost is 3.

提示：

• 1 <= n <= 10000
• wells.length == n
• 0 <= wells[i] <= 10^5
• 1 <= pipes.length <= 10000
• 1 <= pipes[i][0], pipes[i][1] <= n
• 0 <= pipes[i][2] <= 10^5
• pipes[i][0] != pipes[i][1]

---

如果想查看本题目是哪家公司的面试题，请参考以下免费链接： https://leetcode.jp/problemdetail.php?id=1168

解题思路分析：

这道题出的很巧妙。我开始想使用动态规划来做，但没想到思路。看了提示才发现原来是Union-Find并查集问题。

我们将所有住户想象成n个节点，如果能将n个节点都连接起来，并且保证至少一家挖了水井，就可使得所有住户都有水喝。不过题目要求找到最优连接方案，也就是要知道如何连接节点，以及挖几口井的总花费最少。我们先来想第一个问题，比如住户A通过某条水管路线通上了水，住户B也通过某条水管通上了水，那么A和B之间是不需要再进行连线的，否则会花费多余的费用。这样一来，所有连线就不会产生回路，也就是说，最终将所有节点接起来之后，应该是一个树形结构。不过问题来了，题目给出的pipes 数组貌似并不足以让所有节点都能保证联通，也就是说，最后可能会形成多棵树，每棵树的顶点是挖井的住户。那么，这多棵树有没有同一个根节点呢？

答案是有！我们忽略了另外一个节点，即水源。本题，我们可以将水源看做是树的根节点，水源到每一个住户的花费为题目给出的 wells数组。wells 数组的长度为n，即每一家理论上都可以联通到水源。因此通过题目给出的条件我们可以得到以下数量的连线：

int lineCount = wells.length + pipes.length;

通过以上的这些条连线一定可以将所有节点以树形结构连接起来，接下来问题就转化为通过已知节点间cost，如果构建一棵总cost最小的树。

我们将所有连线按照cost由小到大排序，然后循环遍历每一条连线，如果连线上两点已经存在相同的根节点，为了避免回路，他们之间不需要连接。反之，两点间需要连接，并将连接cost加入返回结果。直到循环结束算出总cost即是返回结果。因为数组已经排序过，所以可以保证结果为最优。

最后，判断是否具有相同的根节点，只需要利用Union-find并查集即可。

实现代码：

int[] root;
public int minCostToSupplyWater(int n, int[] wells, int[][] pipes) {
    root=new int[n+1]; // 并查集数组
    for(int i=0;i<n+1;i++) root[i]=i; // 初始时每个节点的根节点为自己
    // 存储所有的边
    int[][] allPipes = new int[pipes.length+wells.length][3];
    // 将每户与水源的连线加入allPipes数组
    for(int i=0;i<n;i++){
        allPipes[i]=new int[]{0, i+1, wells[i]};
    }
    // 将每户间的连线加入allPipes数组
    for(int i=n;i<allPipes.length;i++){
        allPipes[i]=pipes[i-n];
    }
    // 按照cost升序排序
    Arrays.sort(allPipes,(x,y)->x[2]-y[2]);
    int res=0; // 返回结果
    for(int[] p : allPipes){
        int r0=root(p[0]); // 连线上第一个节点的根节点
        int r1=root(p[1]); // 连线上第二个节点的根节点
        if(r0==r1) continue; // 根节点相同，不需此连线
        // 以下均为不在同一根节点下的情况

        // 某一个点的根节点为水源
        if(r0==0 || r1==0){
            // 将另一节点也加到根节点下（Union合并操作）
            root[r0]=0;
            root[r1]=0;
        } else{
            // 将一个根节点加入到另一个根节点下（Union合并操作）
            root[r1]=r0;
        }
        res+=p[2]; // 将当前连线cost加入返回结果
    }
    return res;
}
int root(int i){ // 查找根节点
    while(root[i]!=i) i=root[i];
    return i;
}

本题解法执行时间为29ms。

Runtime: 29 ms, faster than 87.65% of Java online submissions for Optimize Water Distribution in a Village.

Memory Usage: 55.8 MB, less than 100.00% of Java online submissions for Optimize Water Distribution in a Village.

本网站文章均为原创内容，并可随意转载，但请标明本文链接
如有任何疑问可在文章底部留言。为了防止恶意评论，本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言，并会在第一时间对您的留言进行回复！欢迎交流！
本文链接: http://leetcode.jp/leetcode-1168-optimize-water-distribution-in-a-village-解题思路分析/