很早就用过Mybatis Generator，一直觉得没什么可分享的，直到今天工作又要重新配置Mybatis Generator，遇到各种问题各种坑，忍无可忍只能写篇博客压压惊。
之前经常在Maven和Java环境下使用mbg，而且连接的数据库大部分是MySQL 5系，而这一次不仅要将语言切换成kotlin，还要对应Gradle以及MySQL 8系。因此总结下需求即是: 在IntelliJ + Kotlin + Gradle + MySQL8的环境下使用Mybatis Generator自动生成Kotlin文件（包括Entity以及Dao等）。
继续阅读题目大意：
数组的最小偏移量
给你一个由 n 个正整数组成的数组 nums 。
你可以对数组的任意元素执行任意次数的两类操作：
如果元素是 偶数 ，除以 2
例如，如果数组是 [1,2,3,4] ，那么你可以对最后一个元素执行此操作，使其变成 [1,2,3,2]
如果元素是 奇数 ，乘上 2
例如，如果数组是 [1,2,3,4] ，那么你可以对第一个元素执行此操作，使其变成 [2,2,3,4]
数组的 偏移量 是数组中任意两个元素之间的 最大差值 。
返回数组在执行某些操作之后可以拥有的 最小偏移量 。
继续阅读题目大意：
可以到达的最远建筑
给你一个整数数组 heights ，表示建筑物的高度。另有一些砖块 bricks 和梯子 ladders 。
如果当前建筑物的高度 大于或等于 下一建筑物的高度，则不需要梯子或砖块
如果当前建筑的高度 小于 下一个建筑的高度，您可以使用 一架梯子 或 (h[i+1] – h[i]) 个砖块
如果以最佳方式使用给定的梯子和砖块，返回你可以到达的最远建筑物的下标（下标 从 0 开始 ）。
身为一名安卓程序猿，最近被朋友拉来开发一个大型项目，涉及了从infra到server端，再到web前后台，手机app和各种小程序，开发量之大比某些黑厂还令人发指。不过技术发展到今天，能懒则懒应该是一名优秀的程序猿必备的技能，否则你只能苦逼的去做那些重复无聊的工作。今天我们就从搭建一个项目的后台管理系统说起。
后台管理系统是一个大中型项目的标配，标准的后台系统讲究四门功课：对各个数据表进行增删改查。对于这种无聊而又重复性的体力劳动而言，使用代码来生成代码才是聪明的选择。我也是无意间发现了人人开源这个项目，它让我这名懒症重度患者可以继续懒惰下去。。。
下面是人人开源在gitee上的项目地址。
打开上面的链接你会发现里面有6个项目：
这。。。该用哪个呢？我来简单介绍一下这几个项目吧：
renren-security： 正如他介绍文中所写，如果你想搭建一套权限系统，这将是一个不错的选择。不过我没有用过，这里不做评价
SpringBoot2.0-Learning：项目名称即是作者目前的状态，正在学习SB2.0，所以项目还是空的。
renren-fast-adminlte：这就是一款非常强大的开发后台系统的脚手架项目，感兴趣的你可以去尝试一下他的强大。缺点：不是前后端分离设计。另外没有找到相关代码自动生成工具。
接下来是本文的重点了，剩下的三个项目是我最终采用的方案，选择他们的原因有三：
renren-fast： 后台管理系统的后端脚手架项目。主要负责为前端提供API。使用的主要技术栈包括：SpringBoot2.1，MyBatis Plus
renren-fast-vue：后台管理系统的前端脚手架项目。主要负责管理系统的web端页面展示。使用的主要技术栈包括：vue、element-ui
renren-generator：前后端代码生成器。主要负责为上述两个前后端项目生成指定数据表的增删改查代码。
接下来我们开始部署这三个项目。
第一步，克隆或者下载上述三个项目到本地。
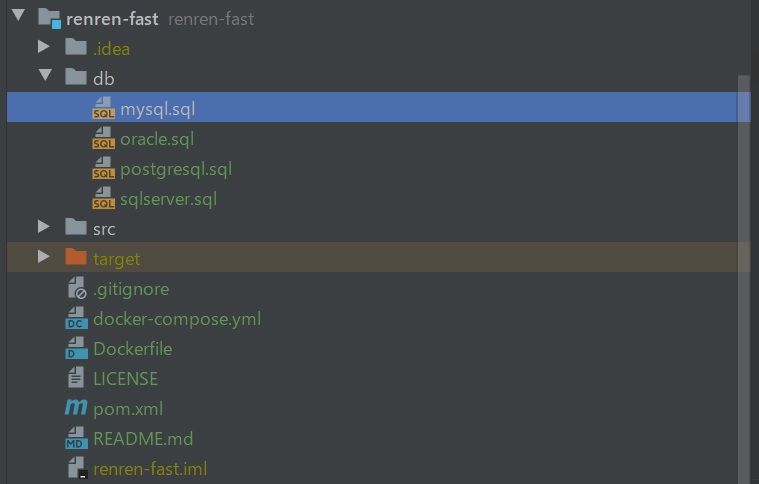
第二步，使用IDEA打开renren-fast后端项目。找到代码中db目录下的sql文，然后打开数据库管理工具，执行该sql语句。这些sql文会为我们的后台系统生成一些基本的表与数据。比如后台管理员表，后台菜单表，后台权限表等等。
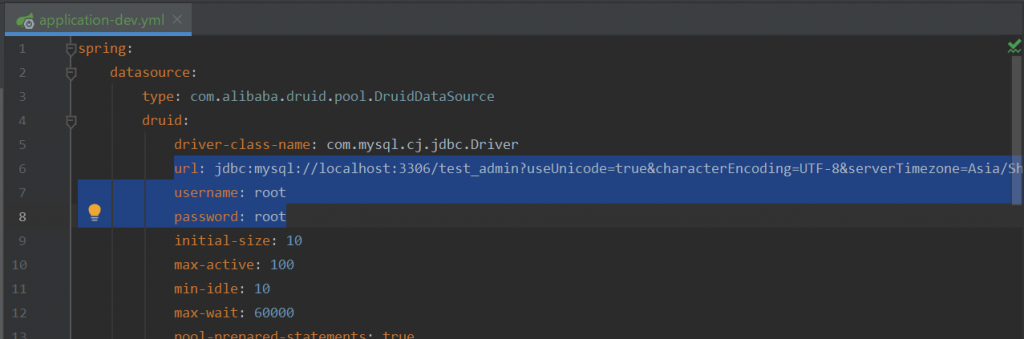
第三步：打开项目配置文件application-dev.yml，修改数据库连接串以及用户名和密码。
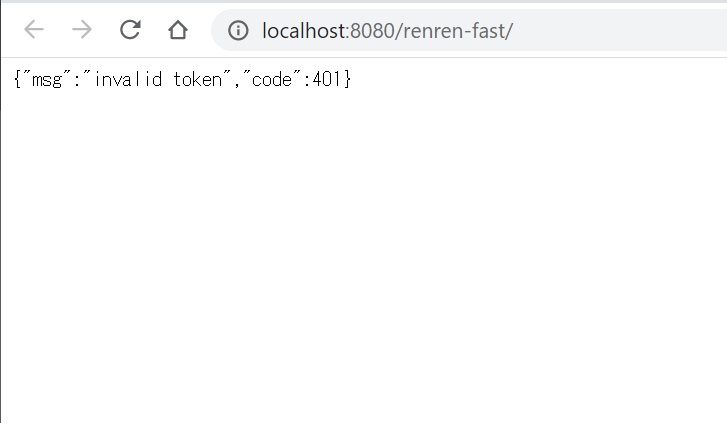
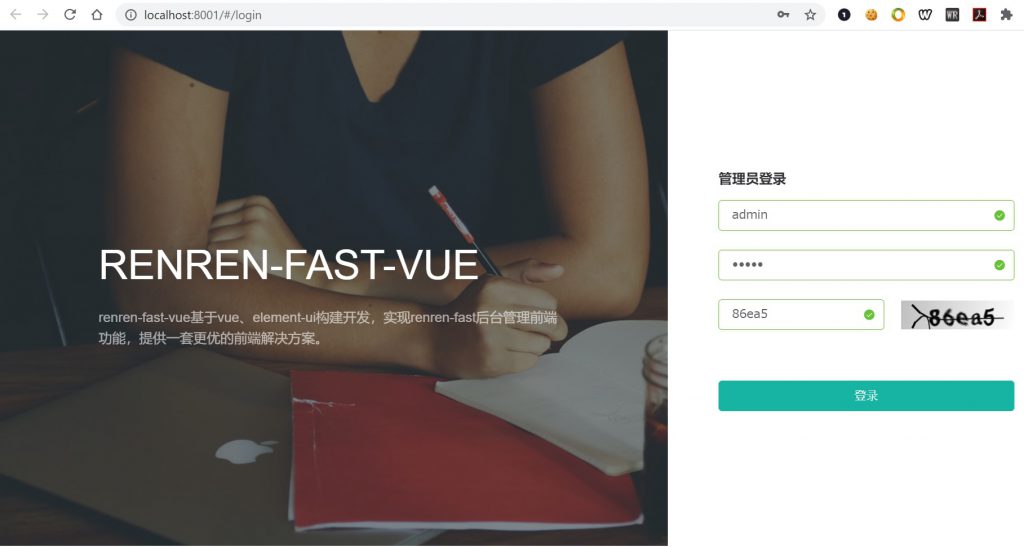
第四步：启动该后端项目。项目会运行在8080端口，启动后，打开浏览器会看到如下画面，至此后端项目配置完成
第五步：使用VS Code打开renren-fast-vue前端项目。该项目无须修改配置。
第六步，下载该vue前端项目相关依赖包，国际惯例，在vs code命令行执行下面的命令（如果你不明白这个命令的意思，没关系你不需要懂，照做即可）。如果你是第一次接触vue，或者你电脑中没有安装过vue开发环境的话，你需要首先安装Node.js（这个并不难，下载个安装包然后安装即可）。我们这里安装Node.js主要为了使用npm命令。
npm install
这里啰嗦几句，有些人在执行npm install后，命令行会报错，主要有2个原因：
原因一：npm install这个命令与安卓的gradle依赖管理以及SpringBoot中的Maven依赖管理类似，他会从前端开发的仓库中下载项目中的相关依赖包并进行安装。Node.js的仓库默认使用海外地址，如果你是中国大陆用户，建议将仓库改为国内地址，修改命令为：
npm config set registry https://registry.npm.taobao.org
原因二：由于node-sass4.9.0安装失败而导致报错。解决办法：清理缓存卸载后重新安装。命令为：
#清理缓存 npm rebuild node-sass #卸载 npm uninstall node-sass #重新安装 npm i node-sass --sass_binary_site=https://npm.taobao.org/mirrors/node-sass/
如果上述过程没有报错，重新执行npm install即可。
第七步，执行下列命令，启动前端程序，至此，前端项目配置完成！使用用户名和密码均为admin的账号即可登录该后台管理系统。
npm run dev
第八步：休息一下，我们简单介绍一下该后台系统。
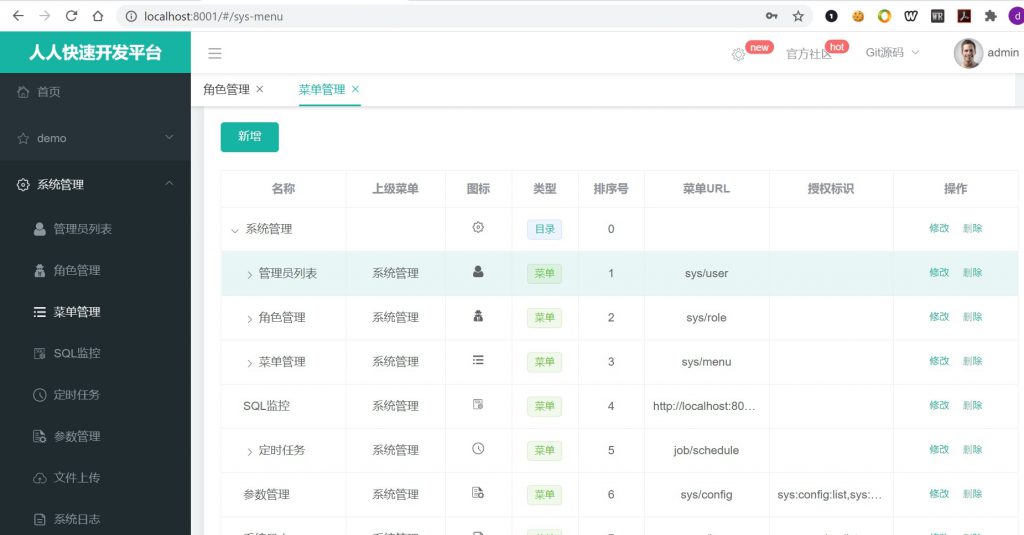
登录进后台管理系统之后，我们发现菜单栏中存在「首页」，「demo」和「系统管理」三个一级目录，而「系统管理」目录下又存在多个子目录，这些功能都是renren-fast-vue为我们自动生成好的脚手架代码。接下来我们需要将项目相关的管理功能添加到系统中，这就需要使用到renren-generator项目来为我们自动生成代码（当然你也可以手动编写）。而生成好的代码如何能够优雅的显示到管理系统中来，那就需要使用到上图中「菜单管理」这个页面了，关于这些操作，我会在下文中逐一介绍。
第九步，使用IDEA打开renren-generator项目并配置。
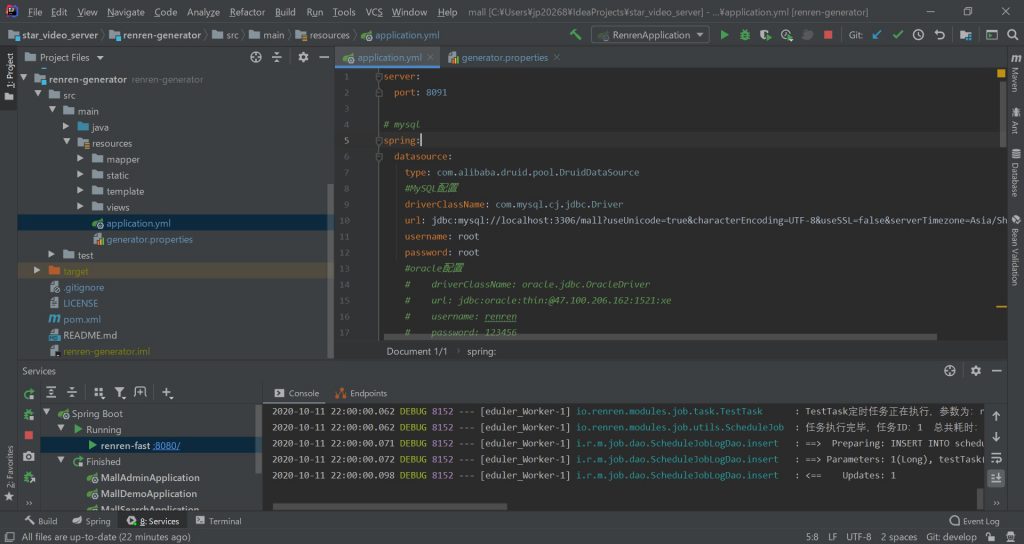
我们需要配置2个文件，首先是\src\main\resources 目录下的application.yml，我们需要修改数据库连接地址以及登录用户名和密码。（我们在第三步配置renren-fast项目时也做过同样的操作。）
另外一个文件是同目录下的generator.properties。
这里主要需要修改文件中以下几个配置：
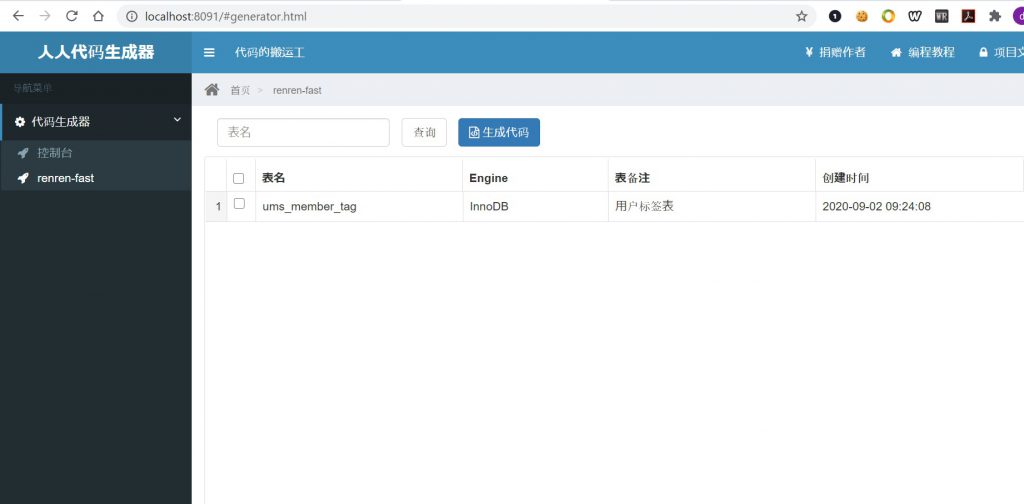
第十步，启动renren-generator项目（使用项目中的RenrenApplication类）。启动之后我们发现该项目存在前端网页，运行地址在8091端口。点击左侧renren-fast菜单，你会看到当前数据库中所有的表（如下图，我当前库中只有一个用户标签表）。
接下来，勾选中想要自动生成代码的数据表，然后点击生成代码即可。生成好的代码会以压缩包（renren.zip）的方式自动下载到本地。解压后，根目录中包含一个main文件夹以及一个或者多个sql文件（取决于你生成了多少张表的代码）。首先我们需要执行该sql文件内的语句，该语句主要是向后台管理系统的菜单表中添加相关数据表的功能。
然后我们需要将main文件夹中自动生成好的代码分别复制到renren-fast-vue前端项目和renren-fast后端项目中去，由于我们使用了与renren项目完全相同的包名配置，因此我们可以将main文件夹直接覆盖到后端项目main文件夹所在的位置。而前端代码位于\renren\main\resources目录之下，该层文件夹中包含mapper和src两个子文件夹，其中只有src是前端项目所需代码，我们将其剪切至前端项目相对应位置覆盖即可。
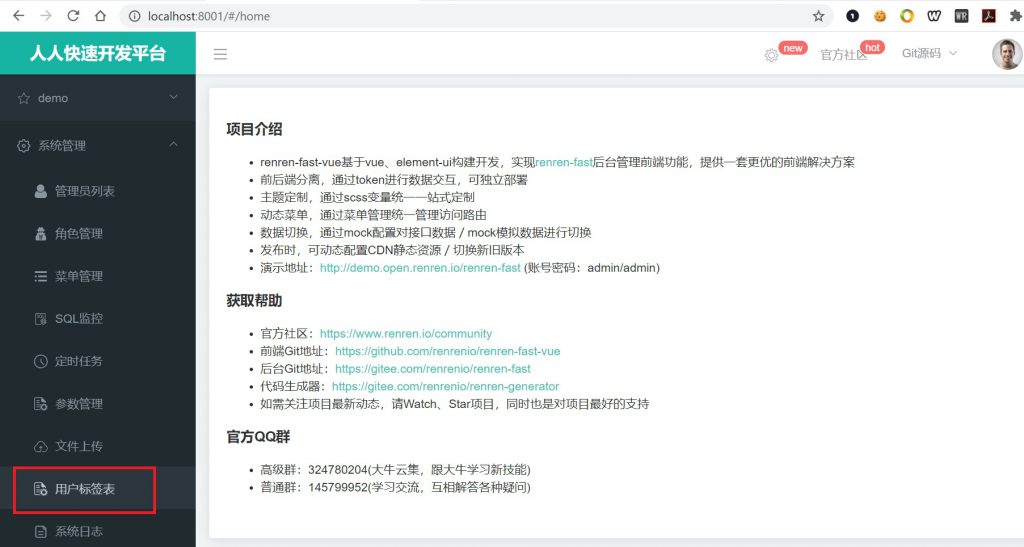
第十一步，重启renren-fast-vue和renren-fast两个项目并重新登录至后台管理系统。此时我们可以发现在系统管理目录下已经自动出现了用户标签表
当然你可能会觉得将用户的管理功能放在系统菜单下并不合适，没关系，你可以通过菜单管理功能来修改每个功能所在的位置
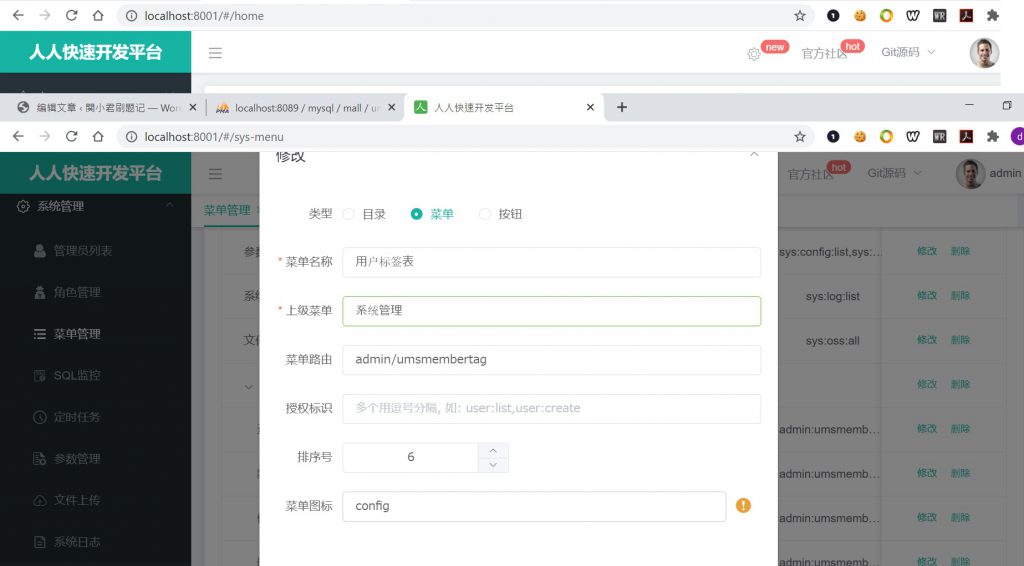
比如上图，当前功能所在的上级菜单为系统管理，我们可以将其修改至其他位置。另外在菜单管理页面我们可以随意添加菜单目录。
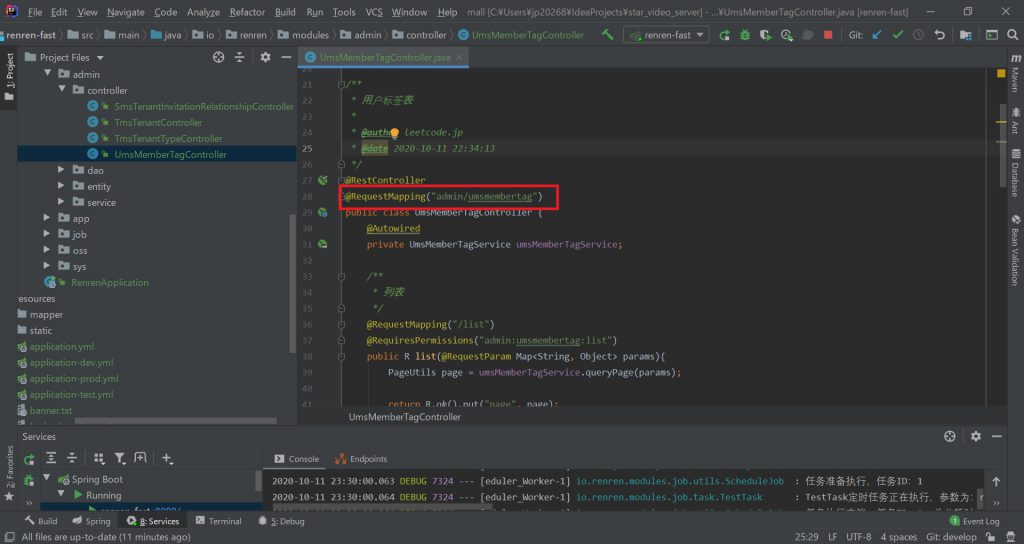
最后顺便说下菜单路由的概念，其实这个设置是自动配置好的，并不需要我们来修改，不过为了更好地理解该项目，我觉得有必要啰嗦一下。其实这个路由指向的是后端代码Controller中对应的地址，比如上图的路由admin/umsmembertag，对应的是下图中红框中的内容：
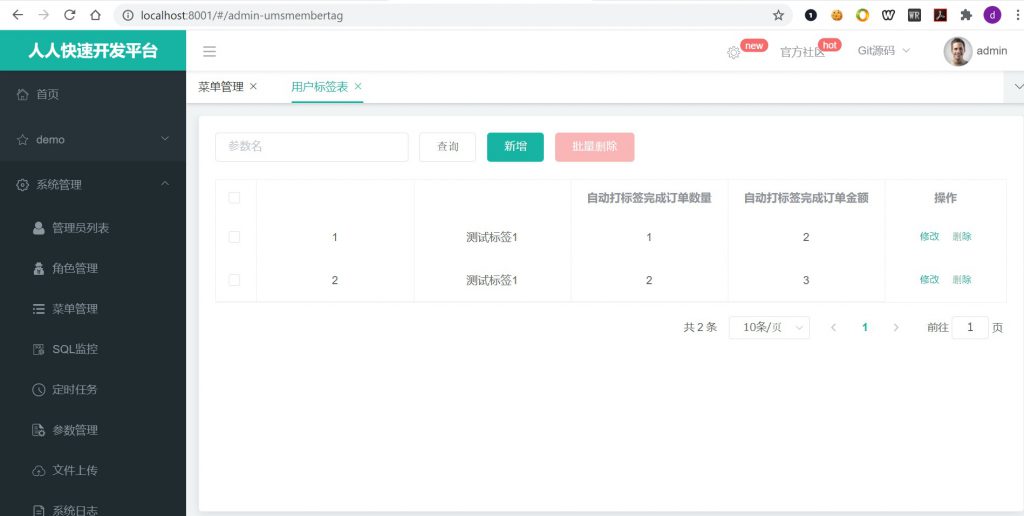
到此为止，教程已经结束，最后我们来看下自动生成好的管理功能长得什么样子？
很显然，基本的增删改查功在我们没有编写一行代码的情况下完美的实现了，这会大幅减少我们不必要的工作量。
也许看完整个教程你会觉得上述过程太过繁琐，那么我只能说你比我还要懒哦哈哈。其实上面大多数配置都是一劳永逸的，只有生成代码的步骤需要每次执行而已，简单的运行代码和复制粘贴最多不会花费5分钟的时间，而你想要自力更生完成上述工作，需要多久你自己心理最清楚（关键是还会出现bug，然后开始各种调试。。。）。
当然，仅凭借上述这个renren的项目还不足以让我快速完成当前的项目，今后有时间，我还会向大家分享更多的实用工具。
以上！
题目大意：
奇偶树
如果一棵二叉树满足下述几个条件，则可以称为 奇偶树 ：
给你二叉树的根节点，如果二叉树为 奇偶树 ，则返回 true ，否则返回 false 。
继续阅读题目大意：
给你一个字符串 s ，请你拆分该字符串，并返回拆分后唯一子字符串的最大数目。
字符串 s 拆分后可以得到若干 非空子字符串 ，这些子字符串连接后应当能够还原为原字符串。但是拆分出来的每个子字符串都必须是 唯一的 。
注意：子字符串 是字符串中的一个连续字符序列。
继续阅读题目大意：
矩阵的最大非负积
给你一个大小为 rows x cols 的矩阵 grid 。最初，你位于左上角 (0, 0) ，每一步，你可以在矩阵中 向右 或 向下 移动。
在从左上角 (0, 0) 开始到右下角 (rows - 1, cols - 1) 结束的所有路径中，找出具有 最大非负积 的路径。路径的积是沿路径访问的单元格中所有整数的乘积。
返回 最大非负积 对109 + 7 取余 的结果。如果最大积为负数，则返回-1 。
注意，取余是在得到最大积之后执行的。
继续阅读题目大意：
二进制矩阵中的特殊位置
给你一个大小为 rows x cols 的矩阵 mat，其中 mat[i][j] 是 0 或 1，请返回 矩阵 mat 中特殊位置的数目 。
特殊位置 定义：如果 mat[i][j] == 1 并且第 i 行和第 j 列中的所有其他元素均为 0（行和列的下标均 从 0 开始 ），则位置 (i, j) 被称为特殊位置。
题目大意：
统计不开心的朋友
给你一份 n 位朋友的亲近程度列表，其中 n 总是 偶数 。
对每位朋友 i，preferences[i] 包含一份 按亲近程度从高到低排列 的朋友列表。换句话说，排在列表前面的朋友与 i 的亲近程度比排在列表后面的朋友更高。每个列表中的朋友均以 0 到 n-1 之间的整数表示。
所有的朋友被分成几对，配对情况以列表 pairs 给出，其中 pairs[i] = [xi, yi] 表示 xi 与 yi 配对，且 yi 与 xi 配对。
但是，这样的配对情况可能会是其中部分朋友感到不开心。在 x 与 y 配对且 u 与 v 配对的情况下，如果同时满足下述两个条件，x 就会不开心：
x 与 u 的亲近程度胜过 x 与 y，且u 与 x 的亲近程度胜过 u 与 v返回 不开心的朋友的数目 。
继续阅读