LEETCODE 308. Range Sum Query 2D – Mutable 解题思路分析

题目大意：

二维区域和检索 – 可变

给你一个 2D 矩阵 matrix，请计算出从左上角 (row1, col1) 到右下角 (row2, col2) 组成的矩形中所有元素的和。

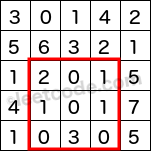
上述粉色矩形框内的，该矩形由左上角 (row1, col1) = (2, 1) 和右下角 (row2, col2) = (4, 3) 确定。其中，所包括的元素总和 sum = 8。

示例：

给定 matrix = [
  [3, 0, 1, 4, 2],
  [5, 6, 3, 2, 1],
  [1, 2, 0, 1, 5],
  [4, 1, 0, 1, 7],
  [1, 0, 3, 0, 5]
]

sumRegion(2, 1, 4, 3) -> 8
update(3, 2, 2)
sumRegion(2, 1, 4, 3) -> 10

提示:

1. 矩阵的值仅可以被update函数更新
2. 您可以假设对update的调用次数和sumRegion函数的调用次数是均匀分布的。
3. 您可以假设 row1 ≤ row2 并且 col1 ≤ col2.

---

如果想查看本题目是哪家公司的面试题，请参考以下免费链接： https://leetcode.jp/problemdetail.php?id=308

解题思路分析：

本题可以采用前缀和来解题，我们之前做过很多一维数组前缀和的问题，本题则是二维数组版本，二维数组前缀和presum[][]，求的是任意一点与[0, 0]点围成的区间内所有数字和。求出前缀和数组之后，对于任意区间内[x1, y1], [x2, y2]的数值和应该等于：

sum([x1,y1],[x2,y2]) = presum[x2][y2]
                     - presum[x1-1][y2]
                     - presum[x2][y1-1]
                     + presum[x1-1][y1-1];

如果感觉公式过于抽象，我们可以参考下图：

上图最左侧红色区域是我们想求和的区域，它的和应该等于蓝色区域减去2个黄色区域的值，而被减去的2个黄色区域存在一个橘红色重复区域（参照上图最右侧），因此还要再加上这个橘色区域即是我们想求的红色区域和。对于蓝色，黄色以及橘色区域都是前缀和数组中存在的值。

解题时，我们需要在构造函数中构建出前缀和数组，sumRegion方法中按照上面的公式求和。update方法中，我们不仅需要更改原矩阵中相对应的数值，另外我们还需要更改前缀和数组中相对应的所有值。即大于等于更新点横坐标并且大于等于更新点纵坐标范围的所有值。

实现代码：

int[][] presum; // 前缀和数组
int[][] m; // 原数组
public NumMatrix(int[][] matrix) {
    m=matrix;
    if(m.length==0) return;
    // 初始化前缀和数组
    presum=new int[matrix.length][matrix[0].length];
    // 计算所有前缀和
    for(int r=0;r<matrix.length;r++){
        int sum=0;
        for(int c=0;c<matrix[0].length;c++){
            sum+=matrix[r][c];
            presum[r][c]=sum+(r>0?presum[r-1][c]:0);
        }
    }
}

public void update(int row, int col, int val) {
    // 查看更新后值的变化
    int diff=val-m[row][col];
    // 更新元素组中对应的数值
    m[row][col]=val;
    // 更新前缀和数组中的值
    for(int r=row;r<m.length;r++){
        for(int c=col;c<m[0].length;c++){
            presum[r][c]+=diff;
        }
    }
}

public int sumRegion(int row1, int col1, int row2, int col2) {
    // 利用前缀和计算当前区域和
    return presum[row2][col2]
        - (row1>0?presum[row1-1][col2]:0)
        - (col1>0?presum[row2][col1-1]:0)
        + (row1>0&&col1>0?presum[row1-1][col1-1]:0);
}

本题解法执行时间为41ms。

Runtime: 41 ms, faster than 20.71% of Java online submissions for Range Sum Query 2D – Mutable.

Memory Usage: 44.6 MB, less than 21.43% of Java online submissions for Range Sum Query 2D – Mutable.

本网站文章均为原创内容，并可随意转载，但请标明本文链接
如有任何疑问可在文章底部留言。为了防止恶意评论，本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言，并会在第一时间对您的留言进行回复！欢迎交流！
本文链接: https://leetcode.jp/leetcode-308-range-sum-query-2d-mutable-解题思路分析/