题目大意:
寻找重复数
给定一个包含 n + 1 个整数的数组 nums,其数字都在 1 到 n 之间(包括 1 和 n),可知至少存在一个重复的整数。假设只有一个重复的整数,找出这个重复的数。
示例 1:
输入: [1,3,4,2,2]
输出: 2示例 2:
输入: [3,1,3,4,2] 输出: 3
说明:
- 不能更改原数组(假设数组是只读的)。
- 只能使用额外的 O(1) 的空间。
- 时间复杂度小于 O(n2) 。
- 数组中只有一个重复的数字,但它可能不止重复出现一次。
如果想查看本题目是哪家公司的面试题,请参考以下免费链接: https://leetcode.jp/problemdetail.php?id=287
解题思路分析:
本题如果没有时间与空间复杂度要求的话,会有很多种解题方式,我们来列举一下:
解法一,暴力解。二层循环每两个数比较,查看是否存在相同数字。时间复杂度n的平方,不推荐。
解法二,排序法。先将数组排序,然后使用每个当前数字与后面一个数字比较查看是否相同。由于排序时的空间复杂度较高,不推荐。
解法三,HashMap。建立一个HashMap,记录每个数字是否出现过,如果当前数字存在于HashMap中,证明该数字是重复数字。空间复杂为n,不推荐。
解法四,二分查找。初始时查找区间为整个数组,取数组的中间位的index,遍历一遍区间,查看小于等于index的数字个数,如果个数大于index,说明重复的数字在1-mid之间,反之在mid+1到n区间。继续二分查找。本解法时间复杂度为nlogn,可行。
解法五,双指针(快慢指针)。这是我最为推荐的一种解法。首先我们可以将数组想象成为一个环状的LinkedList,因为数组中的数字的取值范围在1-n之间,我们可以将任何一位的数字理解为它下一个节点的位置,比如nums[3]=6,也就是下标为3的节点的下一个节点是下标为6的节点。另外注意一点,由于取值范围内不包含0,因此没有节点会指向下标为0的点。我们来看个完整的例子,比如下面这个数组:

将该数组用图来表示可以理解为(下图节点中数字代表该节点下标):
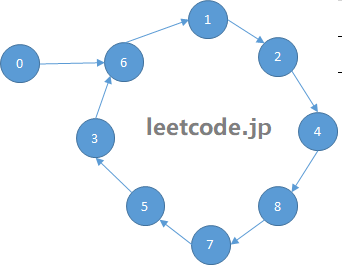
上图中包含一个圆环和一条边[0-6],不难看出边与环的交点6即是本题的重复数字。看到这里,大家可能会产生一个疑问,所有符合本题条件的数组都能构建出类似上面这样的图形吗?答案是肯定的,只不过边的长短以及环的大小会有所不同,但是环与边的交点一定存在。我们可以再看另外一个例子:

相应的图结构如下:
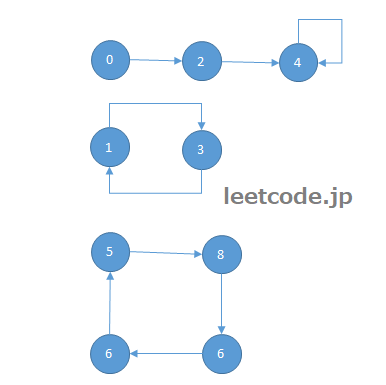
这个例子中,存在一条边与三个环,注意节点4自身可视为一个环,他与边的交点4是本例中的重复节点。另外两个环没有与直线相交,因此不会出现重复点。
这里就不再列举其他的例子了,对于任何符合题意的数组,都可以画出类似以上的结构图,这里我们可以得出三个结论:
- 结构图中一定包含至少一条直线边
- 结构图中一定包含至少一个环
- 边与环的交点为重复节点
接下来我们做一个简单的证明,首先,产生边的原因在于节点0,它可能会指向1-n中的某个节点,但一定没有节点指向他,这样节点0一定不在某个环内,即它是一条环外的边。另外n个节点互相指向,肯定至少能形成一个环。(如果n个节点都指向自己,就能形成n个环)。最后,为什么边与环的交点一定是重复值呢?这也很好证明,环上的任意一个节点都会被其他某一个点指向,这时如果再有环外的一条边上的点指向它,就说明存在两个指向他的点,也就是说数组中有两个不同的下标值都指向该点(若多条边指向他,就说明有多个相同数字)。
以上解释了本题的基本原理,接下来我们要看如何解题,在算法上,这种题目是经典的龟兔赛跑逻辑,我们定义2个指针,快指针和慢指针,两个指针期初同时从下标0出发,慢指针一次走一步,快指针一次走两步,如果路径上不存在环的话,快指针会先走完整条路径,慢指针会使用快指针2倍的时间走完路径。不过本题在上面已经证明过一定存在环,因此,两个指针一定会在环上的某一点相遇(题外话:反过来,如果两指针能相遇,可以证明链表上存在回路,也就是环)。相遇后,我们将其中一个指针的位置不变,另外一个指针回到位置0,然后再以每次前进一步的相同的速度继续走,直到两指针再次相遇时,该相遇点一定是边与环的交点。
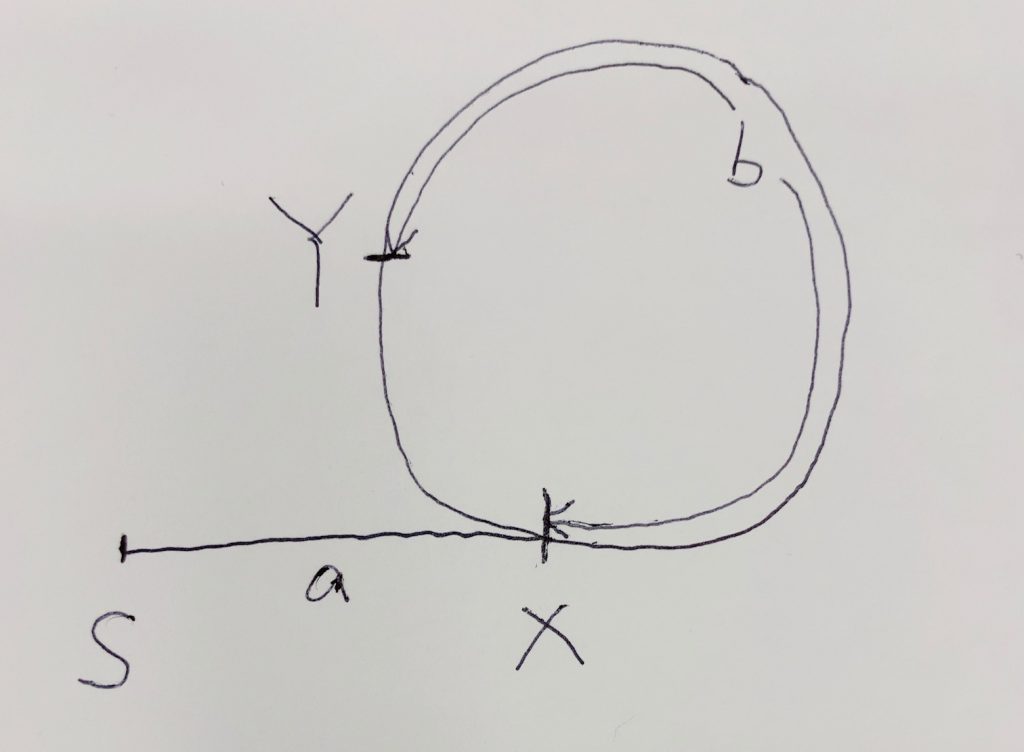
如果你是第一次看到上面这段逻辑可能会一头雾水,其实这是快慢指针的经典应用。这里我简单证明一下,我们设起点S到与环相交点X的距离(步数,每一步走一个距离单位)为a,相交点X到两指针相遇点Y的距离为b,圆环的周长是c,因此,相遇时,慢指针走的步数为a+b,而快指针比慢指针多绕了一圈,因此快指针走的步数为a+b+c,并且我们还知道,快指针每次走两步,而慢指针每次走一步,因此相遇时,快指针走的总步数是慢指针的2倍,即:
a+b+c=2(a+b); // 即: c=a+b;
结论即是,圆环的周长等于:起点S到与圆环相交点X的距离,加上圆环交点X到圆环上两指针相遇点Y距离之和。也就是说,此时从两指针相遇点Y到圆环相交点X的距离等于起点S到X的距离,这样将某一个指针放回起点,再以相同速度前进的话,必然会在X点相遇,该点即是我们要求的答案。
实现代码:
public int findDuplicate(int[] nums) {
// 慢指针走一步
int slow=nums[0];
// 快指针走二步
int fast=nums[nums[0]];
// 两指针同时走,直到首次相遇
while(slow!=fast){
slow=nums[slow];
fast=nums[nums[fast]];
}
// 将快指针放回到起点
fast=0;
// 两指针开始一相同速度前进
// 再次相遇时即为答案
while(slow!=fast){
slow=nums[slow];
fast=nums[fast];
}
return slow;
}本题解法执行时间为0ms。
Runtime: 0 ms, faster than 100.00% of Java online submissions for Find the Duplicate Number.
Memory Usage: 42.7 MB, less than 5.09% of Java online submissions for Find the Duplicate Number.
本网站文章均为原创内容,并可随意转载,但请标明本文链接如有任何疑问可在文章底部留言。为了防止恶意评论,本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言,并会在第一时间对您的留言进行回复!欢迎交流!
本文链接: https://leetcode.jp/leetcode-287-find-the-duplicate-number-解题思路分析/