题目大意:
Given a root of an N-ary tree, you need to compute the length of the diameter of the tree.
The diameter of an N-ary tree is the length of the longest path between any two nodes in the tree. This path may or may not pass through the root.
(Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value.)
Example 1:
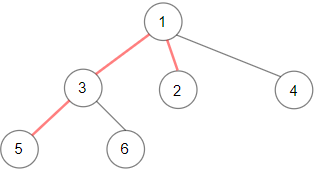
Input: root = [1,null,3,2,4,null,5,6] Output: 3 Explanation: Diameter is shown in red color.
Example 2:
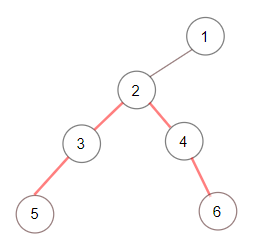
Input: root = [1,null,2,null,3,4,null,5,null,6] Output: 4
Example 3:
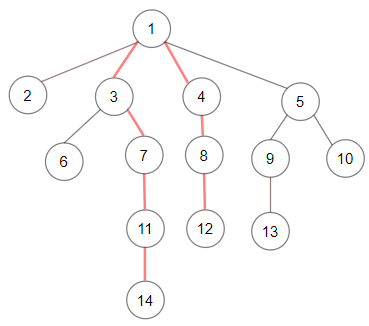
Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] Output: 7
Constraints:
- The depth of the n-ary tree is less than or equal to
1000. - The total number of nodes is between
[0, 10^4].
如果想查看本题目是哪家公司的面试题,请参考以下免费链接: https://leetcode.jp/problemdetail.php?id=1522
解题思路分析:
这道题与之前讲过的 LEETCODE 1245. Tree Diameter 解题思路分析 几乎一模一样。惟一的区别在于题目中的无向树变为了多叉树。但解题原理没有差别。遇到树的题目,多数要考虑到使用dfs或者bfs来解题。本题也不例外,从多叉树顶点开始dfs整棵树,对于任意当前节点,它能组成的最大边长应该是从自身出发的所有路径中最长两条路径长度的和。因此,在每一步dfs中,我们需要记录下当前节点最长两条路径的长度,并求出和sum,使用该sum更新全局最大值。同时返回最长的一条边的长度给上层dfs。全部dfs结束后,找到最大的sum即是结果。
实现代码:
int res=0; // 返回结果
public int diameter(Node root) {
dfs(root); // dfs递归每一个节点
return res; // 返回全局最大值
}
int dfs(Node root){
int max1=0; // 当前节点下距离叶子节点最长的路径
int max2=0; // 当前节点下距离叶子节点次长的路径
for(Node child : root.children){ // 循环每一个子节点
// 递归查看当前子节点到叶子节点的最长路径
// 加一为当前节点到该子节点的距离
int length=dfs(child)+1;
// 使用该距离更新最长路径即次长路径
if(length>=max1){
max2=max1;
max1=length;
}else if(length>=max2){
max2=length;
}
}
// 最长的两个路径之和为通过当前节点的最长路径
// 用该长度更新全局最大长度
res=Math.max(res, max1+max2);
// 返回当前节点下的最大路径
return max1;
}本题解法执行时间为1ms。
Runtime: 1 ms, faster than 47.31% of Java online submissions for Diameter of N-Ary Tree.
Memory Usage: 41.6 MB, less than 8.60% of Java online submissions for Diameter of N-Ary Tree.
本网站文章均为原创内容,并可随意转载,但请标明本文链接如有任何疑问可在文章底部留言。为了防止恶意评论,本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言,并会在第一时间对您的留言进行回复!欢迎交流!
本文链接: https://leetcode.jp/leetcode-1522-diameter-of-n-ary-tree-解题思路分析/