题目大意:
找到N叉树的根节点
给你一个包含N叉树所有节点的列表集合Node[] tree,每个节点都有一个不重复的值。
找出并返回N叉树的根节点
N叉树输入序列以其级别顺序表示,每组子节点由null分隔(请参见示例)。
进阶:你可以使用O(1)的空间复杂度找到根节点吗?
注意:
- 下面例子的输入数据仅为测试使用
- 您将以任意顺序接收N叉树所有节点的列表作为输入。
示例1:
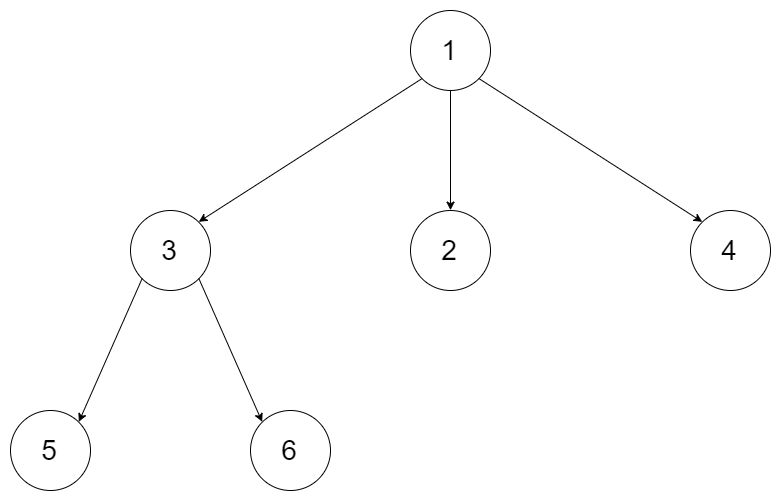
输入: [1,null,3,2,4,null,5,6] 输出: [1,null,3,2,4,null,5,6]
示例2:
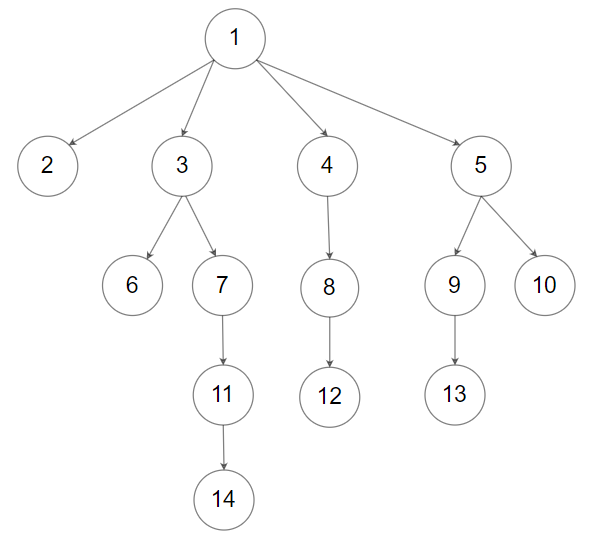
输入: [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] 输出: [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
提示:
- 节点数量在
[1, 5*10^4]之间。 - 每个节点都拥有一个唯一值。
如果想查看本题目是哪家公司的面试题,请参考以下免费链接: https://leetcode.jp/problemdetail.php?id=1506
解题思路分析:
先考虑空间复杂度为O(n)的思路,我们建立一个Set来存储所有节点的所有子节点,最终没有被加入Set的元素一定是根节点。
实现代码:
public Node findRoot(List<Node> tree) {
Set<Integer> set = new HashSet<>(); // 所有子节点
for(Node node : tree){ // 遍历每个节点
for(Node child : node.children){ // 遍历当前节点的子节点
set.add(child.val); // 将子节点加入set
}
}
for(Node node : tree){ // 再次遍历每个节点
// 如果当前节点不存在于set中,当前节点即是根节点
if(!set.contains(node.val)) return node;
}
return null;
}这种思路很好理解,作为根节点,一定不会被加入到Set中,所以最终set中不存在的元素即是根节点。接下来再思考如何使用常数O(1)空间来解题。实际上进阶方法与上一方法的本质是相同的,只不过我们可以使用一个数字代替Set。因为所有节点的值是唯一的,那么我们可以算出所有节点的数值和,并且还可以计算出所有子节点(之前存在set中的所有元素)的数值和,他们的差就是根节点的数值。解题时,为了书写方便,我们建立一个long型数值sum,循环每个节点,累加当前val,然后再减去它所有子节点的val。循环完所有节点后,sum值即是根节点的值。
实现代码:
public Node findRoot(List<Node> tree) {
long sum=0; // 计算根节点val
for(Node node : tree){
sum+=node.val; // 累加当前节点值
for(Node child : node.children){
sum-=child.val; // 减去子节点值
}
}
for(Node node : tree){
if(node.val==sum) return node;
}
return null;
}本题解法执行时间为11ms。
Runtime: 11 ms, faster than 100.00% of Java online submissions for Find Root of N-Ary Tree.
Memory Usage: 50.9 MB, less than 100.00% of Java online submissions for Find Root of N-Ary Tree.
本网站文章均为原创内容,并可随意转载,但请标明本文链接如有任何疑问可在文章底部留言。为了防止恶意评论,本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言,并会在第一时间对您的留言进行回复!欢迎交流!
本文链接: https://leetcode.jp/leetcode-1506-find-root-of-n-ary-tree-解题思路分析/