题目大意:
最多 K 次交换相邻数位后得到的最小整数
给你一个字符串 num 和一个整数 k 。其中,num 表示一个很大的整数,字符串中的每个字符依次对应整数上的各个 数位 。
你可以交换这个整数相邻数位的数字 最多 k 次。
请你返回你能得到的最小整数,并以字符串形式返回。
示例 1:
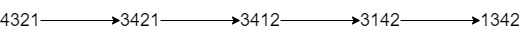
输入:num = "4321", k = 4 输出:"1342" 解释:4321 通过 4 次交换相邻数位得到最小整数的步骤如上图所示。
示例 2:
输入:num = "100", k = 1 输出:"010" 解释:输出可以包含前导 0 ,但输入保证不会有前导 0 。
示例 3:
输入:num = "36789", k = 1000 输出:"36789" 解释:不需要做任何交换。
示例 4:
输入:num = "22", k = 22 输出:"22"
示例 5:
输入:num = "9438957234785635408", k = 23 输出:"0345989723478563548"
提示:
1 <= num.length <= 30000num只包含 数字 且不含有 前导 0 。1 <= k <= 10^9
如果想查看本题目是哪家公司的面试题,请参考以下免费链接: https://leetcode.jp/problemdetail.php?id=1505
解题思路分析:
这道题需要使用贪心算法。试想如果想要将整数变得更小,我们应试图将比较小的数字移动到高位,另外从当前位置移动到高位的cost应该是两个位置的距离差,因此这个差值不能大于k,否则将无法在规定步数内完成移动。基于此原理,解题时我们从最高位开始向后循环,找到一个最小的数字,以及他所在的下标minIndex,注意该数字必须保证与最高位间的距离要小于等于k。然后我们将该数字移动到最高位,并将次高位到minIndex-1间的数字分别向后移动一位(相当于冒泡排序)。此时我们已经确定下来最高位的数字,另外k值已经消耗掉minIndex个单位。接下来,我们再按照上述逻辑去确定次高位的数字,以此类推,直到确定完所谓位置或者当前k值为0时结束操作。以上操作可以使用循环,异可以使用递归完成。
实现代码:
public String minInteger(String num, int k) {
char[] arr=num.toCharArray(); // 为了方便计算,将字符串转为数组
return String.valueOf(help(arr,k, 0)); // 递归求解
}
// arr:数组
// k:当前剩余步数
// index:当前高位
char[] help(char[] arr,int k, int index){
// 如果下标越界或者k为0,返回
if(index==arr.length||k==0) return arr;
// 找出当前高位之后最小的数字以及所在下标
char min=arr[index];
int minIndex=index;
for(int i=index;i<arr.length&&i-index<=k;i++){
if(arr[i]<min){
min=arr[i];
minIndex=i;
}
}
// 将当前高位到minIndex-1间的的数字分别向后移动一位
for(int i=minIndex;i>index;i--){
arr[i]=arr[i-1];
}
// 将最高位设置为最小值(相当于冒泡排序)
arr[index]=min;
// 递归求解次高位
return help(arr,k-(minIndex-index),index+1);
}本题解法执行时间为929ms。
Runtime: 929 ms, faster than 33.33% of Java online submissions for Minimum Possible Integer After at Most K Adjacent Swaps On Digits.
Memory Usage: 43.8 MB, less than 100.00% of Java online submissions for Minimum Possible Integer After at Most K Adjacent Swaps On Digits.
本网站文章均为原创内容,并可随意转载,但请标明本文链接如有任何疑问可在文章底部留言。为了防止恶意评论,本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言,并会在第一时间对您的留言进行回复!欢迎交流!
本文链接: https://leetcode.jp/leetcode-1505-minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits-解题思路分析/