题目大意:
课程安排 IV
你总共需要上 n 门课,课程编号依次为 0 到 n-1 。
有的课会有直接的先修课程,比如如果想上课程 0 ,你必须先上课程 1 ,那么会以 [1,0] 数对的形式给出先修课程数对。
给你课程总数 n 和一个直接先修课程数对列表 prerequisite 和一个查询对列表 queries 。
对于每个查询对 queries[i] ,请判断 queries[i][0] 是否是 queries[i][1] 的先修课程。
请返回一个布尔值列表,列表中每个元素依次分别对应 queries 每个查询对的判断结果。
注意:如果课程 a 是课程 b 的先修课程且课程 b 是课程 c 的先修课程,那么课程 a 也是课程 c 的先修课程。
示例 1:
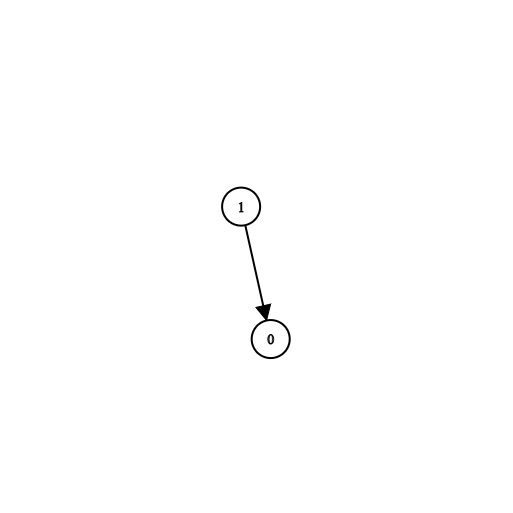
输入:n = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]] 输出:[false,true] 解释:课程 0 不是课程 1 的先修课程,但课程 1 是课程 0 的先修课程。
示例 2:
输入:n = 2, prerequisites = [], queries = [[1,0],[0,1]] 输出:[false,false] 解释:没有先修课程对,所以每门课程之间是独立的。
示例 3:
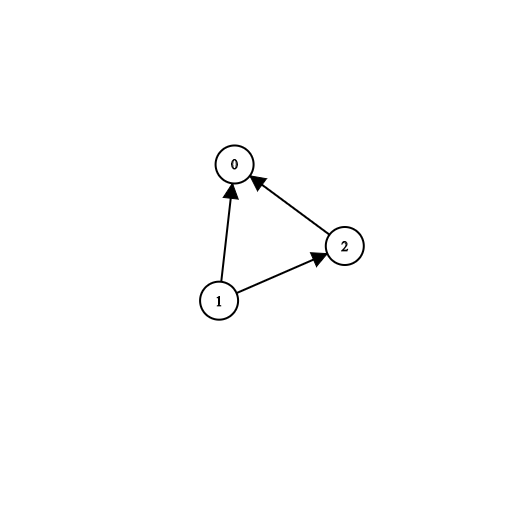
输入:n = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]] 输出:[true,true]
示例 4:
输入:n = 3, prerequisites = [[1,0],[2,0]], queries = [[0,1],[2,0]] 输出:[false,true]
示例 5:
输入:n = 5, prerequisites = [[0,1],[1,2],[2,3],[3,4]], queries = [[0,4],[4,0],[1,3],[3,0]] 输出:[true,false,true,false]
提示:
- 2 <= n <= 100
- 0 <= prerequisite.length <= (n * (n – 1) / 2)
- 0 <= prerequisite[i][0], prerequisite[i][1] < n
- prerequisite[i][0] != prerequisite[i][1]
- 先修课程图中没有环。
- 先修课程图中没有重复的边。
- 1 <= queries.length <= 10^4
- queries[i][0] != queries[i][1]
如果想查看本题目是哪家公司的面试题,请参考以下免费链接: https://leetcode.jp/problemdetail.php?id=1462
解题思路分析:
这是一道不存在回路的有向图问题,对于图的问题采用dfs深度优先搜索来解题非常合适。本题,我们需要先建立出图形结构,按照惯例,图形结构可以采用HashMap或者数组来构建,本题由于课程编号已经固定为0-n,因此相比于Map,采用数组的效率更高。我们定义数组的下标代表课程标号,数组中的值保存该课程的所有直接先修课程列表。
接下来我们循环queries数组,查看每一组课程的先修课关系。我们以当前课程queries[i][1]为起点,dfs查看其所有先修课路径中是否包含目标课程queries[i][0],如果包含,返回true,反之返回false。
最后,由于本题需要判断queries数组中全部的课程对关系,也就是说我们需要以不同或相同的课程作为起点进行多次的dfs调用,这就必将会导致出现重复计算问题,比如1->2->3->4,假设我们计算过4是2的先修课,当再计算1和4的关系时,我们只需要计算出2是1的先修课即可,因为此时已知4是2的先修课,因此可以推导出4也必定是1的先修课。为了避免这种重复计算的发生,此处我们需要引入记忆数组,记录下递归函数已经计算过的结果。
实现代码:
List<Integer>[] map; // 图结构
Boolean[][] memo; // 记忆数组
public List<Boolean> checkIfPrerequisite(int n, int[][] prerequisites, int[][] queries) {
map=new ArrayList[n]; // 初始化图结构数组
memo=new Boolean[n][n]; // 初始化记忆数组
for(int[] p : prerequisites){ // 构建图结构
if(map[p[1]]==null)map[p[1]]=new ArrayList<>();
// 将该先修课保存至当前课程的先修课列表中
map[p[1]].add(p[0]);
}
// 返回结果
List<Boolean> res = new ArrayList<>();
// 循环每一个查询
for(int[] q: queries){
// dfs求解
res.add(dfs(q[1],q[0]));
}
return res;
}
// course:当前课程
// pre:查询目标先修课
// 返回值:pre是否是course的先修课
boolean dfs(int course, int pre){
// 如果当前课程等于先修课,返回true
if(course==pre) return true;
// 如果记忆数组中存在当前解,直接返回
if(memo[course][pre]!=null)return memo[course][pre];
// 获取当前课程的先修课列表
List<Integer> list=map[course];
// 如果列表为空,返回false
if(list==null) return false;
// 返回结果
boolean res=false;
// 遍历每一个先修课
for(int c : list){
// 将先修课作为课程传入dfs子问题
if(dfs(c,pre)){
// 如果返回结果为true,说明找到了目标先修课pre
res=true;
break; // 退出
}
}
memo[course][pre]=res; // 将当前结果保存至记忆数组
return res;
}本题解法执行时间为29ms。
Runtime: 29 ms, faster than 90.52% of Java online submissions for Course Schedule IV.
Memory Usage: 43.8 MB, less than 100.00% of Java online submissions for Course Schedule IV.
本网站文章均为原创内容,并可随意转载,但请标明本文链接如有任何疑问可在文章底部留言。为了防止恶意评论,本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言,并会在第一时间对您的留言进行回复!欢迎交流!
本文链接: https://leetcode.jp/leetcode-1462-course-schedule-iv-解题思路分析/