LEETCODE 1411. Number of Ways to Paint N × 3 Grid 解题思路分析

题目大意：

给 N x 3 网格图涂色的方案数

你有一个 n x 3 的网格图 grid ，你需要用红，黄，绿三种颜色之一给每一个格子上色，且确保相邻格子颜色不同（也就是有相同水平边或者垂直边的格子颜色不同）。

给你网格图的行数 n 。

请你返回给 grid 涂色的方案数。由于答案可能会非常大，请你返回答案对 10^9 + 7 取余的结果。

示例 1：

输入：n = 1
输出：12
解释：总共有 12 种可行的方法：

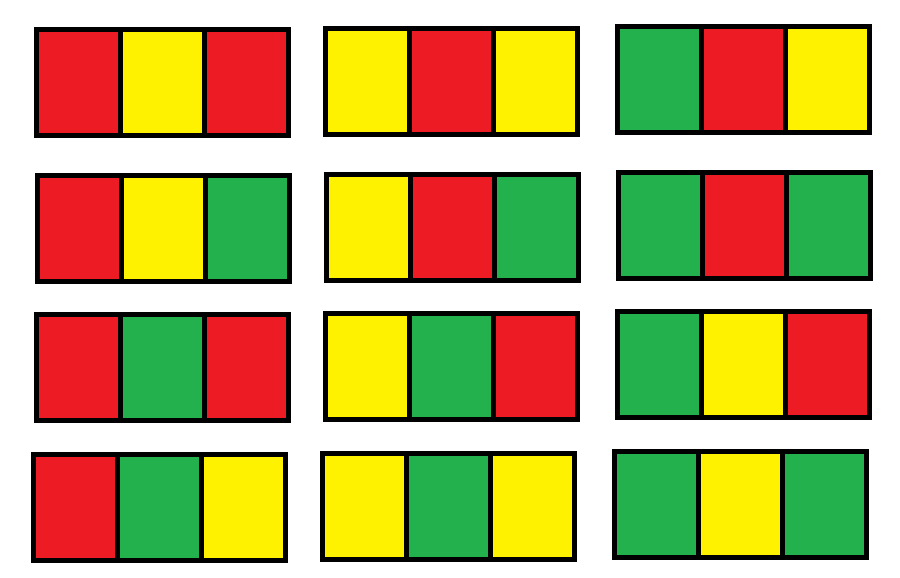
示例 2：

输入：n = 2
输出：54

示例 3：

输入：n = 3
输出：246

示例 4：

输入：n = 7
输出：106494

示例 5：

输入：n = 5000
输出：30228214

提示：

n == grid.length
grid[i].length == 3
1 <= n <= 5000

如果想查看本题目是哪家公司的面试题，请参考以下免费链接： https://leetcode.jp/problemdetail.php?id=1411

解题思路分析：

本周参加周赛的状态实际上还是不错的，前三题只用了不到20分钟，但读完第四题也就是本题之后，肚子突然翻江倒海，让我不得不在厕所耗费了近50分钟。再回来做本题时已毫无状态，只能用了一个很low的解法算是蒙混过关，今后有时间我会重新优化一下本题的写法。

回到本题，实际上本题的思路还是非常清晰的，由于一行只有3列，因此保证每一行内不重复的排列方式一共有12种。推导过程为；第一个格子有3种选择，第二个格子由于不能与相邻的第一个格子相同，因此只有2种选择，同理，第三个格子不能与相邻的第二个格子颜色相同，因此也只有2种选择。3乘以2再乘以2等于12种。这12种组合实际上就是题目例子1中给出的排列方式：

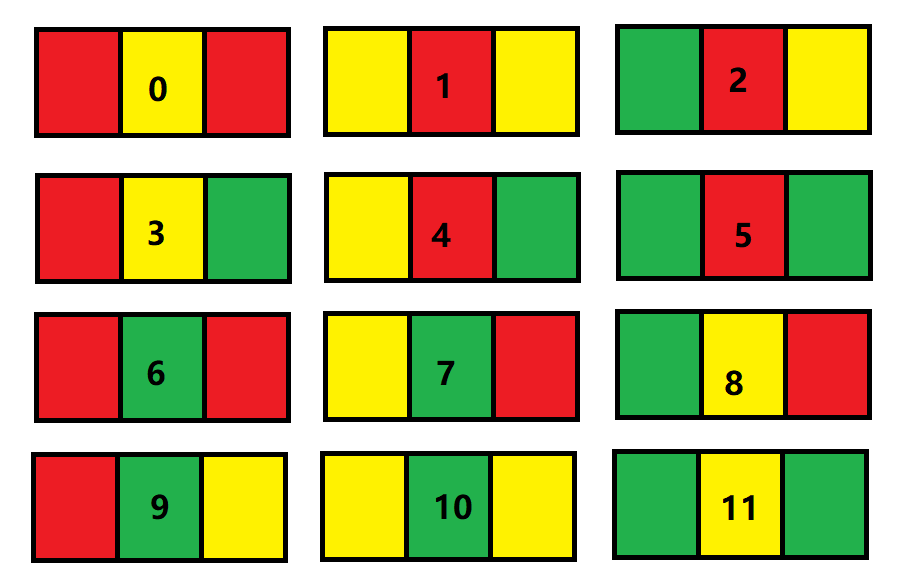
当存在n行时，当前行能够选取上述哪几种组合，完全取决于相邻的上一行的情况。为了方便描述，我们为上述12中方式编号为0-11（如何编号，看个人喜好），之后，我们分别找出每一个图形的相邻行能摆放哪些图形。比如编号0的下方可以连接编号1，2，4，5，10，这样会保证他们之间每一个相邻的格子都不重复。再比如编号7下面可以连接2，3，5，11。由于总体的数量不是很多，因此我用肉眼，统计出了每一种编号下方可以连接的其他编号。我们使用一个boolean型数组来记录他们之间的关系，boolean[i][j]表示编号i和j是否可以相连。

boolean[][] map = new boolean[12][12];
map[0][1]=true;
map[0][2]=true;
map[0][4]=true;
map[0][5]=true;
map[0][10]=true;

map[1][0]=true;
map[1][3]=true;
map[1][6]=true;
map[1][8]=true;
map[1][11]=true;

map[2][0]=true;
map[2][3]=true;
map[2][6]=true;
map[2][7]=true;

map[3][1]=true;
map[3][2]=true;
map[3][7]=true;
map[3][10]=true;

map[4][0]=true;
map[4][6]=true;
map[4][8]=true;
map[4][9]=true;

map[5][0]=true;
map[5][6]=true;
map[5][7]=true;
map[5][9]=true;
map[5][10]=true;

map[6][1]=true;
map[6][2]=true;
map[6][4]=true;
map[6][5]=true;
map[6][11]=true;

map[7][2]=true;
map[7][3]=true;
map[7][5]=true;
map[7][11]=true;

map[8][1]=true;
map[8][3]=true;
map[8][9]=true;
map[8][10]=true;

map[9][4]=true;
map[9][5]=true;
map[9][8]=true;
map[9][11]=true;

map[10][0]=true;
map[10][3]=true;
map[10][5]=true;
map[10][8]=true;
map[10][11]=true;

map[11][1]=true;
map[11][6]=true;
map[11][7]=true;
map[11][9]=true;
map[11][10]=true;

接下来我们可以将本题想象为一个多叉树，多叉树的第一层有12个节点。然后每个节点都有多个子节点，这里的子节点实际上就是能与当前编号相连接的其他编号，我们只要统计出第n层存在节点的数量，就是我们本题的结果。

解题时可以使用dfs来递归所有路径。实现代码：

int[][] memo;
public int numOfWays(int n) {
    memo=new int[12][n];
    boolean[][] map = new boolean[12][12];
    map[0][1]=true;
    map[0][2]=true;
    map[0][4]=true;
    map[0][5]=true;
    map[0][10]=true;
    map[1][0]=true;
    map[1][3]=true;
    map[1][6]=true;
    map[1][8]=true;
    map[1][11]=true;
    map[2][0]=true;
    map[2][3]=true;
    map[2][6]=true;
    map[2][7]=true;
    map[3][1]=true;
    map[3][2]=true;
    map[3][7]=true;
    map[3][10]=true;
    map[4][0]=true;
    map[4][6]=true;
    map[4][8]=true;
    map[4][9]=true;
    map[5][0]=true;
    map[5][6]=true;
    map[5][7]=true;
    map[5][9]=true;
    map[5][10]=true;
    map[6][1]=true;
    map[6][2]=true;
    map[6][4]=true;
    map[6][5]=true;
    map[6][11]=true;
    map[7][2]=true;
    map[7][3]=true;
    map[7][5]=true;
    map[7][11]=true;
    map[8][1]=true;
    map[8][3]=true;
    map[8][9]=true;
    map[8][10]=true;
    map[9][4]=true;
    map[9][5]=true;
    map[9][8]=true;
    map[9][11]=true;
    map[10][0]=true;
    map[10][3]=true;
    map[10][5]=true;
    map[10][8]=true;
    map[10][11]=true;
    map[11][1]=true;
    map[11][6]=true;
    map[11][7]=true;
    map[11][9]=true;
    map[11][10]=true;
    long res=0;
    for(int i=0;i<12;i++){
        res+=help(map,i,1,n);
    }
    return (int)(res%1000000007);
}

int help(boolean[][] map, int preRowType, int row,int n){
    if(row==n) return 1;
    if(memo[preRowType][row]>0) return memo[preRowType][row];
    long count=0;
    for(int i=0;i<12;i++){
        if(map[preRowType][i]){
            count+=help(map,i,row+1,n);
        }
    }
    int res = (int)(count%1000000007);
    memo[preRowType][row]=res;
    return res;
}

本题解法执行时间为27ms。

Runtime: 27 ms, faster than 26.23% of Java online submissions for Number of Ways to Paint N × 3 Grid.

Memory Usage: 39.2 MB, less than 100.00% of Java online submissions for Number of Ways to Paint N × 3 Grid.

本网站文章均为原创内容，并可随意转载，但请标明本文链接
如有任何疑问可在文章底部留言。为了防止恶意评论，本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言，并会在第一时间对您的留言进行回复！欢迎交流！
本文链接: https://leetcode.jp/leetcode-1411-number-of-ways-to-paint-n-x-3-grid-解题思路分析/

LEETCODE 1411. Number of Ways to Paint N × 3 Grid 解题思路分析

发表评论取消回复

站内搜索

近期文章

功能

站内搜索

LEETCODE 1411. Number of Ways to Paint N × 3 Grid 解题思路分析

发表评论 取消回复

站内搜索

近期文章

标签

功能

站内搜索

发表评论取消回复