题目大意:
二叉树中的列表
给你一棵以 root 为根的二叉树和一个 head 为第一个节点的链表。
如果在二叉树中,存在一条一直向下的路径,且每个点的数值恰好一一对应以 head 为首的链表中每个节点的值,那么请你返回 True ,否则返回 False 。
一直向下的路径的意思是:从树中某个节点开始,一直连续向下的路径。
示例 1:
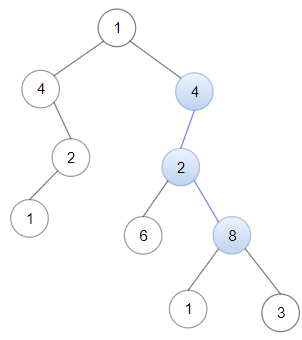
输入:head = [4,2,8], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3] 输出:true 解释:树中蓝色的节点构成了与链表对应的子路径。
示例 2:
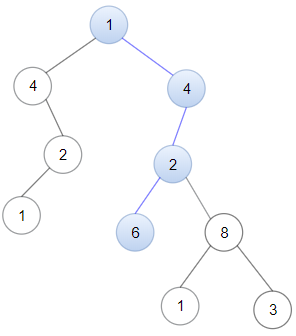
输入:head = [1,4,2,6], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3] 输出:true
示例 3:
输入:head = [1,4,2,6,8], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3] 输出:false 解释:二叉树中不存在一一对应链表的路径。
提示:
- 二叉树和链表中的每个节点的值都满足 1 <= node.val <= 100 。
- 链表包含的节点数目在 1 到 100 之间。
- 二叉树包含的节点数目在 1 到 2500 之间。
如果想查看本题目是哪家公司的面试题,请参考以下免费链接: https://leetcode.jp/problemdetail.php?id=1367
解题思路分析:
遇到二叉树和链表题目时,使用dfs或者说递归来解题是最为高效的方式。本题我们需要dfs二叉树上的每一个节点,然后以当前节点为起点查看是否能找到与链表完全相同的路径。与链表进行比对时,同样需要使用到dfs递归操作。如果二叉树当前节点与链表当前节点不相同,那么说明无法找到匹配的路径,返回false。如果相同,我们查看二叉树的右子节点是否为空,如果不为空,dfs递归至二叉树右子节点与链表下一节点。同理,我们还可以dfs递归至二叉树左子节点以及链表下一节点。两条线路只要有一条返回true即可。递归的终止条件为当链表的下一节点为null时,返回true。
实现代码:
public boolean isSubPath(ListNode head, TreeNode root) {
// dfs求解
return dfs(head,root);
}
boolean dfs(ListNode head, TreeNode root){
// 查看以当前root节点为起点,是否能找到与链表完全一致的路径。
// 如果能找到,返回true。
if(check(head, root)) return true;
// 如果当前节点找不到与链表相同的路径,
// dfs递归至左子节点,如果能找到,返回true。
if(root.left!=null&&dfs(head, root.left)) return true;
// 若还不能找到,dfs递归至右子节点,如果能找到,返回true。
if(root.right!=null&&dfs(head, root.right)) return true;
// 若还不能找到,返回false。
return false;
}
// 查看以二叉树当前节点为起点,是否能找到与链表相同的路径
boolean check(ListNode head, TreeNode root){
// 如果链表当前节点等于二叉树当前节点
if(head.val==root.val){
// 若链表不存在下一节点,说明链表已经遍历结束,返回true
if(head.next==null) return true;
// 如果链表还有下一节点,并且二叉树存在左子节点,
// 利用链表的下一节和二叉树的左子节点继续递归
if(root.left!=null&&check(head.next, root.left)) return true;
// 如果链表还有下一节点,并且二叉树存在右子节点,
// 利用链表的下一节和二叉树的右子节点继续递归
if(root.right!=null&&check(head.next, root.right)) return true;
}
return false;
}本题解法执行时间为1ms。
Runtime: 1 ms, faster than 99.73% of Java online submissions for Linked List in Binary Tree.
Memory Usage: 41.7 MB, less than 100.00% of Java online submissions for Linked List in Binary Tree.
本网站文章均为原创内容,并可随意转载,但请标明本文链接如有任何疑问可在文章底部留言。为了防止恶意评论,本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言,并会在第一时间对您的留言进行回复!欢迎交流!
本文链接: https://leetcode.jp/leetcode-1367-linked-list-in-binary-tree-解题思路分析/