题目大意:
参加考试的最大学生数
给你一个 m * n 的矩阵 seats 表示教室中的座位分布。如果座位是坏的(不可用),就用 ‘#’ 表示;否则,用 ‘.’ 表示。
学生可以看到左侧、右侧、左上、右上这四个方向上紧邻他的学生的答卷,但是看不到直接坐在他前面或者后面的学生的答卷。请你计算并返回该考场可以容纳的一起参加考试且无法作弊的最大学生人数。
学生必须坐在状况良好的座位上。
示例 1:
输入:seats = [["#",".","#","#",".","#"], [".","#","#","#","#","."], ["#",".","#","#",".","#"]] 输出:4 解释:教师可以让 4 个学生坐在可用的座位上,这样他们就无法在考试中作弊。
示例 2:
输入:seats = [[".","#"], ["#","#"], ["#","."], ["#","#"], [".","#"]] 输出:3 解释:让所有学生坐在可用的座位上。
示例 3:
输入:seats = [["#",".",".",".","#"], [".","#",".","#","."], [".",".","#",".","."], [".","#",".","#","."], ["#",".",".",".","#"]] 输出:10 解释:让学生坐在第 1、3 和 5 列的可用座位上。
提示:
- seats 只包含字符 ‘.’ 和’#’
- m == seats.length
- n == seats[i].length
- 1 <= m <= 8
- 1 <= n <= 8
如果想查看本题目是哪家公司的面试题,请参考以下免费链接: https://leetcode.jp/problemdetail.php?id=1349
解题思路分析:
本题又是一道典型的动态规划问题,对于任何一个座位,如果它不是损坏座椅,并且它的的左方,右方,左前方,右前方,左后方,右后方都没有人,该座位才能坐人,否则不能安排考生入座。解题时,我们可以按照从上至下的顺序逐行安排座位,对于当前行的任意一个座位,如果能坐的话,我们可以选择安排一个座位,或者不安排座位。如果该座位不能安排考生,则肯定不能安排座位,最终选择出一种最优解即可。
我们使用递归方式解题的话,可以定义这样一个递归方法:
int help(int row, int col)
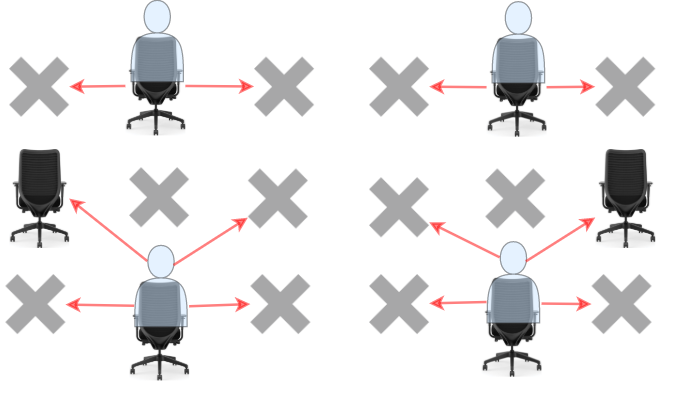
参数row和col代表当前行和列,递归函数返回值为当前点后面的位置能安排多少座位。递归函数按照逐行方式递归,即每次列数加一,当列数大于矩阵列数时,列数变为0,行数加一。递归顺序如下图:
递归函数内的逻辑为:
// 如果当前位置可以安排座位 count1 = 1 + help(下一个位置); // 如果当前位置不安排座位 // 注意有以下两种情况可以不安排座位: // 1. 当前位置不能安排座位 // 2. 当前位置可以安排座位,但选择不安排座位 count2 = help(下一个位置); return max(count1, coun2)
思考到这里,本以为这道题目是一道非常简单的动态规划问题(或者说是递归问题),但是我忽略了一点,如何设计记忆数组。之前我们做过很多DP题目,记忆数组(dp数组)的定义很简单,使用递函数的参数即可,比如本题,我们可以定义记忆数组为:
int[][] memo;
其中memo[row][col]代表该位置后面能够安排的最多座位数。看起来很有道理,但实际上是完全行不通的。分析到这里,我们有必要来搞明白本题不能这样定义的根本原因所在!对于之前的大部分dp题目,不论题目原型是矩阵或是数组,亦或是树状图,他们的每个节点的状态是不会改变的,而本题则不同,一个点是否能安排座位,不仅仅取决于当前座位是否损坏(这个条件是不变的),而且还要取决于它的左右以及斜前后方六个位置上是否已经安排了其他考生,正是因为这个条件是不能确定,因此对于同一个位置,该位置后面能够安排的最多座位数,会随着其他位置是否安排考生这个条件的改变而发生改变,这样一来,记忆数组中memo[row][col]值的意义就不复存在了。我们举个例子来说明一下,比如:

比如问号处为当前位置,它的上一行安排了两个座位,因此它之后能安排的最多座位数是4(安排方式如右边两图的黄色格子)。但是,如果它的上一行的安排方式是下面这种情况:
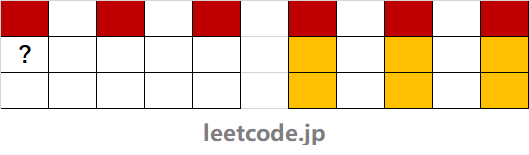
那么问号后面最多可以安排上6个座位(右图黄色格子)。所以问号处的记忆数组就无法发挥作用。这样一来,本题就无法使用记忆数组了吗?看了一下题目给出的数据规模,矩阵大小最大为8乘8的格子,不使用记忆数组的情况下,java语言应该是可以勉强通过极限测试的,但效率非常低。因此我们还是要考虑如何设计记忆数组来提高代码效率。
我们看下下面这张图:
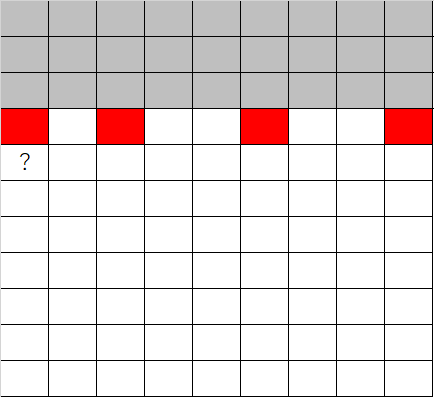
对于问号处之后的位置一共最多能安排多少座位,其实取决于与他相邻上一行座位的摆放情况。与其再之前的行的座位情况是无关的(灰色区域),理解了这一点,对于我们设计记忆数组是非常关键的。如果我们知道了上一行座椅摆放情况下,就能够确定当前位置之后能够安排的最多座位数量,这样,遇到相同情况时,我们就可以直接使用记忆数组中的数值了。因此记忆数组应该设计为:
int[][] memo;
其中 memo[row][state]代表,第row行的摆放情况是state时,第 row+1行及之后的 位置一共最多摆放座位的数量。这里state可以使用二进制方式来记录某一行座位的摆放,0代表没有座位,1代表安排了座位。比如:101001代表了第0,2,5列上安排了座位。
实现代码:
int[][] memo; // 记忆数组
public int maxStudents(char[][] seats) {
// state代表某一行安排座椅的情况,用二进制表示
int state = 1;
// 求出state的最大值,即当前行每一列都安排座位的情况
for(int c=0;c<seats[0].length;c++){
state = ((1<<c) | state);
}
// 利用行数和state的最大值初始化记忆数组
memo=new int[seats.length][state];
// 递归求解,从第0行第0列开始递归
// 即求出第0行第0列以及它后面一共最多可以安排座椅的最大数量
return help(seats,0,0,0);
}
// seats:矩阵
// r:当前行
// c:当前列
// rowState:当前行安排的座位状态
// 返回值:当前位置及之后的位置一共可以安排座位的做大数量
int help(char[][] seats, int r, int c, int rowState){
// 如果当前是某一行的第一列
if(c==0&&r>0){
// 当前为第一列时,rowState值为上一行完整的座位安排情况
// 查看记忆数组中是否存在上一行该座位安排情况的值
// 如果存在,返回记忆数组中的值
if(memo[r-1][rowState]>0) return memo[r-1][rowState];
}
// 当前位置字符
char ch = seats[r][c];
// 计算下一个递归位置
int nextR=r, nextC=c;
// 如果当前列加一小于总列数
if(c+1<seats[0].length){
// 下一位置列数加一,行数不变
nextC=c+1;
}else{ // 如果当前列加一超出总列数
// 下一位置列数为0
nextC=0;
// 下一位置行数加一
nextR=r+1;
}
// 查看当前位置是否可以安排座位
boolean canSit=canSit(seats,r,c);
// 如果当前位置是矩阵最后一格(递归终止条件)
if(nextR==seats.length){
// 如果能安排座位返回1,否则返回0
return canSit?1:0;
}
// 第一种选择,为当前位置安排座位
int count1=0;
// 如果当前位置能安排座位
if(canSit(seats,r,c)){
// 将当前位置设置为S,代表安排了座位
seats[r][c]='S';
// 递归求解下一个位置以及之后位置一共能安排的做多座位数
// 再加上一代表当前位置安排了一个座位
count1=1+help(seats, nextR,nextC,c==0?1:((rowState<<1)|1));
// 递归结束后,将当前位置还原成原始字符,以便之后查询其他递归可能
seats[r][c]=ch;
}
// 第二种选择,不为当前位置安排座位
int count2=help(seats, nextR,nextC,c==0?0:((rowState<<1)|0));
// 两种选择的最大值为当前结果
int res = Math.max(count1,count2);
// 如果当前是某一行的首列
if(c==0&&r>0){
// 将当前结果计入记忆数组
memo[r-1][rowState]=res;
}
return res;
}
// 判断当前位置是否可以安排座位
boolean canSit(char[][] seats, int r, int c){
// 如果当前是损坏座位,返回false
if(seats[r][c]=='#') return false;
// 左前方有座位,当前不能安排座位
if(r>0&&c>0){
if(seats[r-1][c-1]=='S') return false;
}
// 右前方有座位,当前不能安排座位
if(r>0&&c<seats[0].length-1){
if(seats[r-1][c+1]=='S') return false;
}
// 右方有座位,当前不能安排座位
if(c>0){
if(seats[r][c-1]=='S') return false;
}
// 因为递归顺序是从上至下,从左至右,因此右方和下方都是空位不需判断
return true;
}本题解法执行时间为1ms。
Runtime: 1 ms, faster than 99.82% of Java online submissions for Maximum Students Taking Exam.
Memory Usage: 37.3 MB, less than 100.00% of Java online submissions for Maximum Students Taking Exam.
本网站文章均为原创内容,并可随意转载,但请标明本文链接如有任何疑问可在文章底部留言。为了防止恶意评论,本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言,并会在第一时间对您的留言进行回复!欢迎交流!
本文链接: https://leetcode.jp/leetcode-1349-maximum-students-taking-exam-解题思路分析/