LEETCODE 1292. Maximum Side Length of a Square with Sum Less than or Equal to Threshold 解题思路分析

题目大意：

元素和小于等于阈值的正方形的最大边长

给你一个大小为 m x n 的矩阵 mat 和一个整数阈值 threshold。

请你返回元素总和小于或等于阈值的正方形区域的最大边长；如果没有这样的正方形区域，则返回 0 。

示例 1：

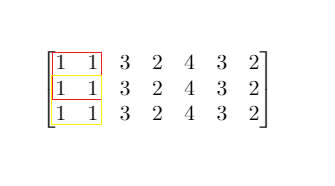
输入：mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4
输出：2
解释：总和小于 4 的正方形的最大边长为 2，如图所示。

示例 2：

输入：mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1
输出：0

示例 3：

输入：mat = [[1,1,1,1],[1,0,0,0],[1,0,0,0],[1,0,0,0]], threshold = 6
输出：3

示例 4：

输入：mat = [[18,70],[61,1],[25,85],[14,40],[11,96],[97,96],[63,45]], threshold = 40184
输出：2

提示：

• 1 <= m, n <= 300
• m == mat.length
• n == mat[i].length
• 0 <= mat[i][j] <= 10000
• 0 <= threshold <= 10^5

---

如果想查看本题目是哪家公司的面试题，请参考以下免费链接： https://leetcode.jp/problemdetail.php?id=1292

解题思路分析：

这道题最简单的思路就是以每一个点为顶点向右下画正方形，正方形起始边长为1，即当前点。最长边长为当前点到左边与下边的最短距离。正方形边长每增加一格，其实是增加了下图的两个矩形部分（红色与蓝色部分），计算新的正方形内所有数字和即原正方形的和加上新增两个矩形内数字和。如果该和小于等于 threshold ，用当前边长更新最大边长即可。如果和大于 threshold ，结束当前循环，移动到下一个顶点继续向右下画正方形。

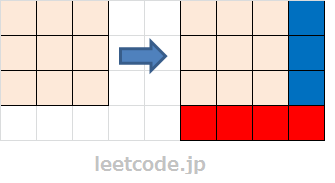
计算新增矩形范围的数字和，我们可以利用前缀和数组来优化算法，避免每次都要循环累加一次矩形范围内所有数字。

实现代码：

public int maxSideLength(int[][] mat, int threshold) {
    // 每一行前缀和
    int[][] preSumR = new int[mat.length][mat[0].length];
    // 每一列前缀和
    int[][] preSumC = new int[mat.length][mat[0].length];
    // 矩阵内最小数
    int minNum=Integer.MAX_VALUE;
    for(int r=0;r<mat.length;r++){
        for(int c=0;c<mat[0].length;c++){
            minNum=Math.min(minNum,mat[r][c]);
            if(c==0) preSumR[r][c]=mat[r][c];
            else preSumR[r][c]=preSumR[r][c-1]+mat[r][c];
            if(r==0) preSumC[r][c] = mat[r][c];
            else preSumC[r][c]=preSumC[r-1][c]+mat[r][c];
        }
    }
    // 如果矩阵最小数大于threshold，返回0
    if(minNum>threshold) return 0;
    // 返回结果，默认最小为1
    int res=1;
    // 循环每一个点，以该点作为起点向右下画正方形
    for(int r=0;r<mat.length;r++){
        for(int c=0;c<mat[0].length;c++){
            // 当前点数值
            int sum=mat[r][c];
            // 当前点能向右下画的最大正方形边长
            int maxLength = Math.min(mat.length-r,mat[0].length-c);
            // 如果当前点数值大于threshold或者能画的最大边长小于等于res
            // 不必判断当前点，移动到下一个顶点
            if(sum>threshold||maxLength<=res) continue;
            // 以当前顶点向右下画正方形，每次边长加一
            for(int i=1;i<maxLength;i++){
                // 累加新增区域内数字和
                sum+=preSumR[r+i][c+i]-preSumR[r+i][c]+mat[r+i][c];
                sum+=preSumC[r+i-1][c+i]-preSumC[r][c+i]+mat[r][c+i];
                // 如果和大于threshold退出当前循环
                if(sum>threshold) break;
                // 更新最大边长
                res=Math.max(res, i+1);
            }
        }
    }
    return res;
}

本题解法执行时间为37ms。

Runtime: 37 ms, faster than 60.49% of Java online submissions for Maximum Side Length of a Square with Sum Less than or Equal to Threshold.

Memory Usage: 61.8 MB, less than 100.00% of Java online submissions for Maximum Side Length of a Square with Sum Less than or Equal to Threshold.

本网站文章均为原创内容，并可随意转载，但请标明本文链接
如有任何疑问可在文章底部留言。为了防止恶意评论，本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言，并会在第一时间对您的留言进行回复！欢迎交流！
本文链接: https://leetcode.jp/leetcode-1292-maximum-side-length-of-a-square-with-sum-less-than-or-equal-to-threshold-解题思路分析/