题目大意:
统计封闭岛屿的数目
有一个二维矩阵 grid ,每个位置要么是陆地(记号为 0 )要么是水域(记号为 1 )。
我们从一块陆地出发,每次可以往上下左右 4 个方向相邻区域走,能走到的所有陆地区域,我们将其称为一座「岛屿」。
如果一座岛屿 完全 由水域包围,即陆地边缘上下左右所有相邻区域都是水域,那么我们将其称为 「封闭岛屿」。
请返回封闭岛屿的数目。
示例 1:
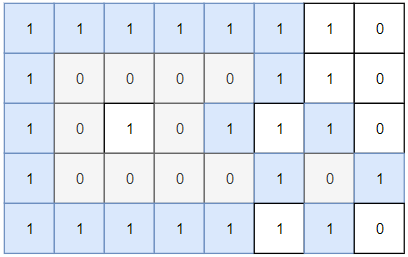
输入:grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]] 输出:2 解释: 灰色区域的岛屿是封闭岛屿,因为这座岛屿完全被水域包围(即被 1 区域包围)。
示例 2:
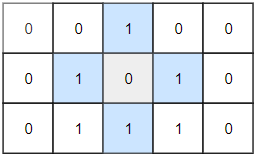
输入:grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]] 输出:1
示例 3:
输入:grid = [[1,1,1,1,1,1,1],
[1,0,0,0,0,0,1],
[1,0,1,1,1,0,1],
[1,0,1,0,1,0,1],
[1,0,1,1,1,0,1],
[1,0,0,0,0,0,1],
[1,1,1,1,1,1,1]]
输出:2提示:
1 <= grid.length, grid[0].length <= 1000 <= grid[i][j] <=1
如果想查看本题目是哪家公司的面试题,请参考以下免费链接: https://leetcode.jp/problemdetail.php?id=1254
解题思路分析:
Leetcode中海岛的题目还是比较多的,之前的文章也多次讲过类似的题目。平心而论,如果面试时遇到这类题目我们应该感到庆幸,毕竟这种题型难度并不大。
看过我之前文章的话,大家应该想到,海岛题应该联想到使用dfs或者bfs求解,无论是哪种搜索方式,我们可以对搜索过的位置进行染色,代表已经访问过,避免之后重复搜索。本题的思路也同理,不论bfs或是dfs的时间复杂度是相同的,但是考虑到bfs会使用到Queue存储数据,因此在效率上会略低于dfs,此外bfs的空间复杂度也要更高一些。所以本题推荐使用dfs求解。(文章最后也会给出bfs解题版本)
解题步骤:
- 循环地图上所有点,如果当前点为0,说明是某个岛屿的一部分,开始dfs,将整个岛屿染色成为2(区别于其他未访问岛屿和海洋),当dfs到某一个坐标为地图边缘时,将返回结果设为false,如果dfs过程中没有遇到地图边缘,返回true。dfs结束后,如果返回值为true,将封闭岛屿个数加一。
- 继续循环地图上所有点,跳过值为1和2的点,如果当前点为0,重复执行第1步,直到循环结束。
实现代码(dfs):
// 可以走的四个方向
int[][] directions=new int[][]{{1,0},{-1,0},{0,1},{0,-1}};
public int closedIsland(int[][] grid) {
int res=0; // 返回结果
for(int r=0;r<grid.length;r++){ // 循环地图每一个点
for(int c=0;c<grid[0].length;c++){
if(grid[r][c]!=0){ // 当前点不是0,跳过
continue;
}
// dfs当前点所在的整个岛屿
// 如果是封闭岛屿,返回结果加一
if(dfs(grid, r, c)){
res++;
}
}
}
return res;
}
// dfs当前点所在岛屿的所有点
//
// grid为地图
// r和c为当前点坐标
// 返回结果表示当前岛屿是否是封闭岛屿
boolean dfs(int[][] grid, int r, int c){
boolean res=true;
// 如果当前点在地图边缘,返回结果设置为false
if(r==0||r==grid.length-1||c==0||c==grid[0].length-1){
res=false;
}
// 将当前点染色为2
grid[r][c]=2;
// 向四个方向dfs
for(int[] direction : directions){
// 得到下一个点的坐标
int row=r+direction[0],col=c+direction[1];
// 如果下个点的坐标在地图范围内,并且该点的值为0
// 说明该点是与当前点相连的同一岛屿,可以继续dfs
if(row>=0&&row<grid.length
&&col>=0&&col<grid[0].length
&&grid[row][col]==0){
// dfs结果如果为false,将返回结果更新为false
res = dfs(grid, row, col)&&res;
}
}
return res;
}本解法运行时间为2ms。
Runtime: 2 ms, faster than 88.78% of Java online submissions for Number of Closed Islands.
Memory Usage: 43 MB, less than 100.00% of Java online submissions for Number of Closed Islands.
解法二,bfs
由于本解法效率不如dfs,因此不再详细讲解,仅供参考。
int[][] directions=new int[][]{{1,0},{-1,0},{0,1},{0,-1}};
public int closedIsland(int[][] grid) {
int res=0;
for(int r=1;r<grid.length-1;r++){
for(int c=1;c<grid[0].length-1;c++){
if(grid[r][c]!=0){
continue;
}
boolean isValid=true;
Queue<int[]> q = new LinkedList<>();
q.offer(new int[]{r,c});
while(q.size()>0){
int[] p = q.poll();
grid[p[0]][p[1]]=2;
if(p[0]==0||p[1]==0||
p[0]==grid.length-1||p[1]==grid[0].length-1){
isValid=false;
}
for(int[] direction : directions){
int row=p[0]+direction[0],col=p[1]+direction[1];
if(row>=0&&row<grid.length
&&col>=0&&col<grid[0].length
&&grid[row][col]==0){
q.offer(new int[]{row,col});
}
}
}
if(isValid){
res++;
}
}
}
return res;
}bfs解法的运行时间为10ms。
Runtime: 10 ms, faster than 11.22% of Java online submissions for Number of Closed Islands.
Memory Usage: 44.7 MB, less than 100.00% of Java online submissions for Number of Closed Islands.
本网站文章均为原创内容,并可随意转载,但请标明本文链接如有任何疑问可在文章底部留言。为了防止恶意评论,本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言,并会在第一时间对您的留言进行回复!欢迎交流!
本文链接: https://leetcode.jp/leetcode-1254-number-of-closed-islands-解题思路分析/