题目大意:
查找集群内的「关键连接」
数据中心有 n 台服务器,分别按从 0 到 n-1 的方式进行了编号。
它们之间以「服务器到服务器」点对点的形式相互连接组成了一个内部集群,其中连接 connections 是无向的。
从形式上讲,connections[i] = [a, b] 表示服务器 a 和 b 之间形成连接。任何服务器都可以直接或者间接地通过网络到达任何其他服务器。
「关键连接」是在该集群中的重要连接,也就是说,假如我们将它移除,便会导致某些服务器无法访问其他服务器。
请你以任意顺序返回该集群内的所有 「关键连接」。
示例 1:
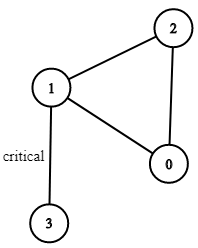
输入:n = 4, connections = [[0,1],[1,2],[2,0],[1,3]] 输出:[[1,3]] 解释:[[3,1]] 也是正确的。
提示:
1 <= n <= 10^5
n-1 <= connections.length <= 10^5
connections[i][0] != connections[i][1]
不存在重复的连接
如果想查看本题目是哪家公司的面试题,请参考以下免费链接: https://leetcode.jp/problemdetail.php?id=1192
解题思路分析:
这是一道高难度题目,如果不了解tarjan算法,很难想到合理的思路。 tarjan算法讲起来太过于繁琐,本人也不是非常精通,就本题来讲,需要知道一个关键点即是:如果N个节点可以形成一个闭环,那么切掉闭环上任意一条边是不影响其连通的。反之这N个节点是一条线(直线或折线),那么任意一条边切断就会将这条线分为2段,这条被切断的边即是本题中提到的「关键连接」。
所以如何才能找到这些关键连接呢?tarjan算法的核心是dfs深度优先搜索。dfs的起点并不重要,理论上从任意一点开始搜索都会遍历完整个图上的所有节点。我们需要定义一个深度变量,代表该节点到起始节点的距离。初始化时,将所有节点的深度定义为-1。起点深度为0。dfs的返回值表示子孙节点往下连接到的最小深度。dfs开始后,每到达一个没被访问过的节点时,它的深度加一,继续以当前节点向后dfs。
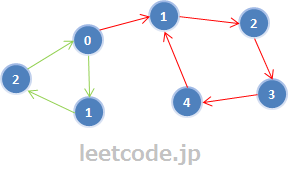
比如上图,每个节点的数字代表距离起始节点的深度。从0开始,遍历完所有节点可以dfs出两条线路(还存在其他dfs方式)。先看绿色dfs线路,起点是0节点,结束也是0节点,说明0在绿色线路的闭环上,因此,绿色线路上任意一条边被删除都不会影响这三个节点相连通。
然而红色路线则不同,起点是0节点,终点是1节点,说明0节点并不在红色线路的闭环上。前文已经说过,如果不在闭环上时,那么当前节点与下一节点之间的连线就是一条「关键连接」。
所以我们可以总结出来,如果dfs的终点位置的深度大于当前节点的深度,那么当前节点与其后一节点间的连线即是一个答案。换句话说,所有大于当前节点深度的都视为自身的子节点,而小于当前深度的都是父节点(深度比较不限于当前dfs路径)。如果dfs终点位于自身子节点,那么当前节点不在闭环之中,反之则在。再举个例子,比如红色线路上的节点2,dfs的终点在1,1是2的父节点,因此2在闭环之中,2-3之间不是关键连接。
基本思路捋清了,我们看下如何编码。
- 先把题目给的线路列表connections转化成图。
- 定义dfs方法,返回值为当前节点dfs终点的最小深度。为什么要返回最小深度,这一点非常关键,我在写代码时思考了很久。看下下面的例子。
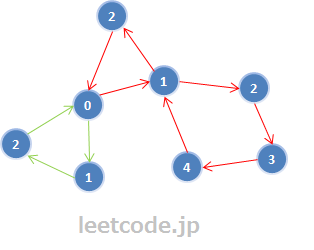
还是以0节点为起始节点,我们看红色线路。首先在0节点位置向下dfs节点1,节点1存在两个分支,终点分别是节点1和节点0。
int dfs(int current){
//current = 0;
dfs(1) = 1; or dfs(1) == 0;
}如果dfs(1)为1,说明0不在红色闭环上,而返回0则代表0在红色闭环上,因此我们应该返回较小的深度给上一层节点。
最后还有一些细节问题需要注意,看下完整的实现代码吧。
List<List<Integer>> res = new ArrayList<>(); // 返回结果
int[] deepArray; // 深度数组
ArrayList<Integer>[] map; // 结构图
public List<List<Integer>> criticalConnections(int n, List<List<Integer>> connections) {
deepArray = new int[n]; // 初始化深度数组
Arrays.fill(deepArray, -1); // 所有节点初始深度为-1
map = new ArrayList[n]; // 初始化结构图map[i]代表节点i可以连通哪些节点
for(int i=0;i<n;i++){
map[i] = new ArrayList<>();
}
// 构建路径图
for(List<Integer> connection : connections){
map[connection.get(0)].add(connection.get(1));
map[connection.get(1)].add(connection.get(0));
}
dfs(0, 0, 0); // 开始dfs
return res;
}
// current为当前节点
// previous为前节点
// deep为当前深度
// 返回值为当前节点所有dfs路径终点的最小深度
private int dfs(int current, int previous, int deep){
deepArray[current] = deep; // 将当前深度存入深度数组
int result = Integer.MAX_VALUE; // 返回值
for(int i : map[current]){ // 遍历当前节点能走的所有节点
if(i == previous){ // 不能走回头路
continue;
}
int endDeep; // dfs终点深度
if(deepArray[i]==-1){ // 深度为-1的点没走过,可以dfs
endDeep = dfs(i, current, deep+1);
// 如果深度大于当前深度,说明当前点不在闭环上
// 当前点与下一节点i之间的连线为答案之一
if(endDeep > deep){
List<Integer> list = new ArrayList<>();
list.add(current);
list.add(i);
res.add(list);
}
}else{
// i节点深度不为-1,说明已经走过,i节点为dfs终点
endDeep = deepArray[i];
}
// 更新最小深度
result = Math.min(result, endDeep);
}
return result; // 返回最小深度
}本题解法用时98ms。(多次提交在95ms-110ms之间)
Runtime: 98 ms, faster than 88.34% of Java online submissions for Critical Connections in a Network.
Memory Usage: 137.5 MB, less than 100.00% of Java online submissions for Critical Connections in a Network.
本网站文章均为原创内容,并可随意转载,但请标明本文链接如有任何疑问可在文章底部留言。为了防止恶意评论,本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言,并会在第一时间对您的留言进行回复!欢迎交流!
本文链接: https://leetcode.jp/leetcode-1192-critical-connections-in-a-network-解题思路分析/