LEETCODE 1091. Shortest Path in Binary Matrix 解题思路分析

题目大意：

二进制矩阵中的最短路径

在一个 N × N 的方形网格中，每个单元格有两种状态：空（0）或者阻塞（1）。

一条从左上角到右下角、长度为 k 的畅通路径，由满足下述条件的单元格 C_1, C_2, ..., C_k 组成：

1. 相邻单元格 C_i 和 C_{i+1} 在八个方向之一上连通（此时，C_i 和 C_{i+1} 不同且共享边或角）
2. C_1 位于 (0, 0)（即，值为 grid[0][0]）
3. C_k 位于 (N-1, N-1)（即，值为 grid[N-1][N-1]）
4. 如果 C_i 位于 (r, c)，则 grid[r][c] 为空（即，grid[r][c] == 0）

返回这条从左上角到右下角的最短畅通路径的长度。如果不存在这样的路径，返回 -1 。

示例 1：

输入：[[0,1],[1,0]]

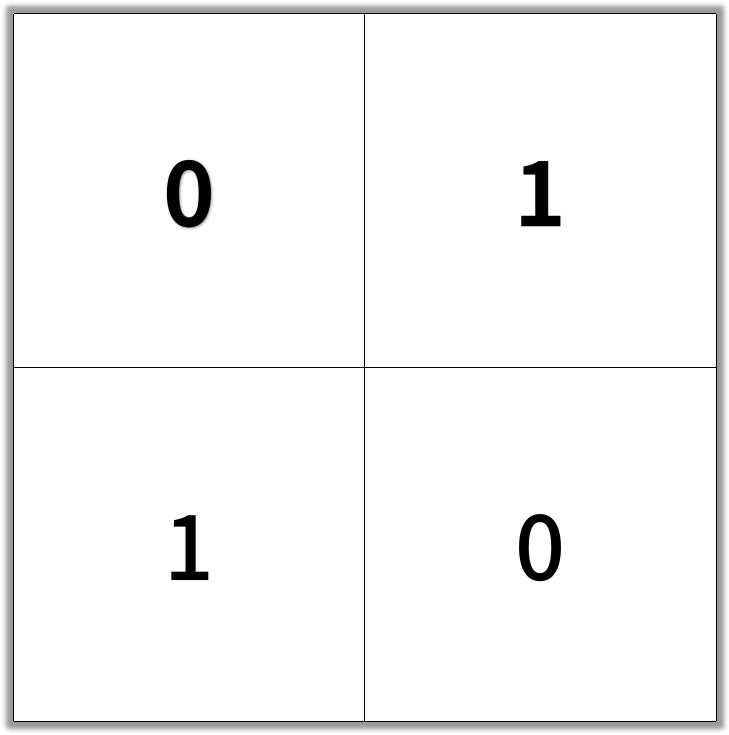
输出：2

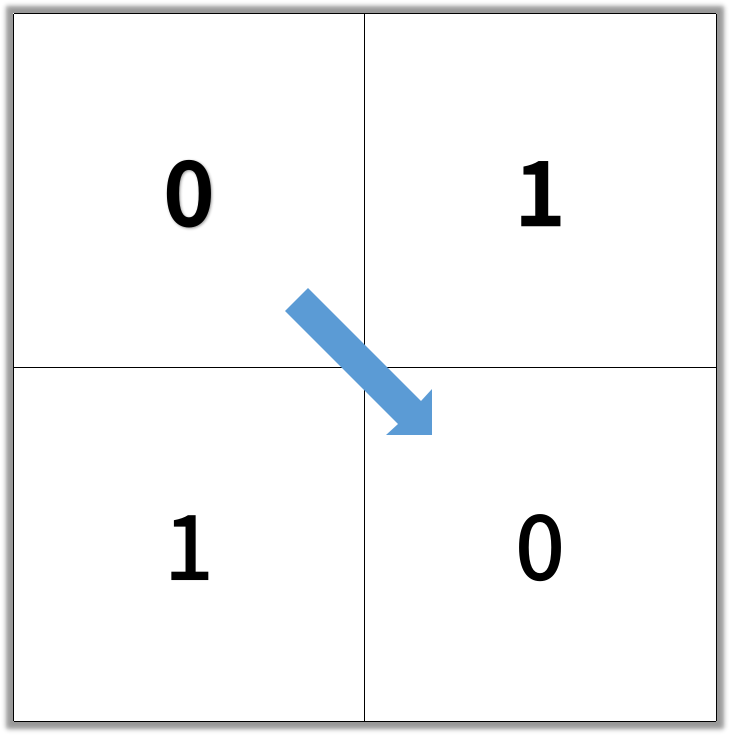
示例 2：

输入：[[0,0,0],[1,1,0],[1,1,0]]

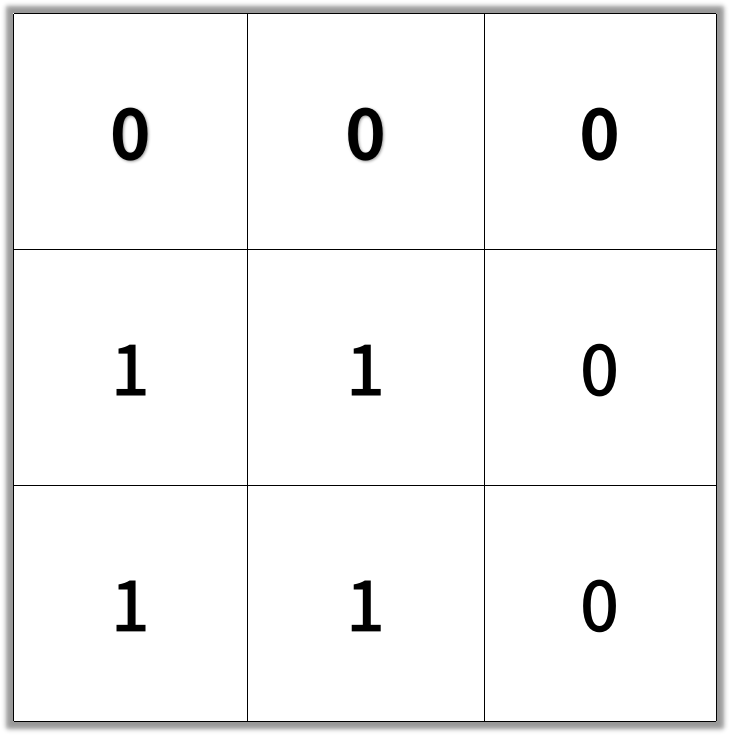
输出：4

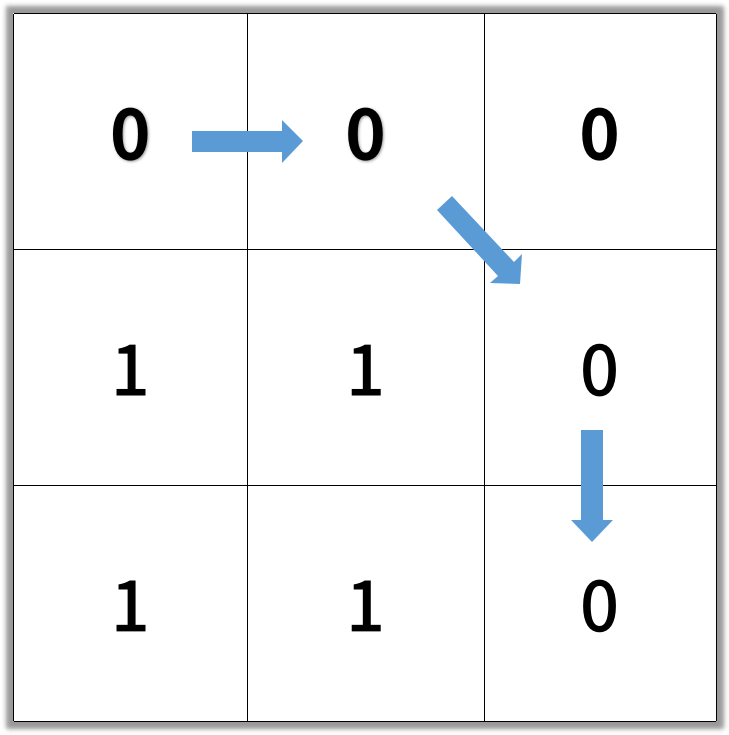
提示：

1. 1 <= grid.length == grid[0].length <= 100
2. grid[i][j] 为 0 或 1

---

如果想查看本题目是哪家公司的面试题，请参考以下免费链接： https://leetcode.jp/problemdetail.php?id=1091

解题思路分析：

看到矩阵和最短距离的题目，我们应该养成下意识想到BFS的好习惯。本题也不例外。题目巴拉巴拉说了很多，其实就是想在矩阵上找到一条最短路径连接左上角和右下角。条件是保证这条路径上所有的点都是0。

之前的文章已经讲过很多bfs的题目，思路大同小异。这里再简单啰嗦一下bfs。首先我们选取一些特征一致的点作为起始目标，然后从这些目标开始向四周扩散一步，四周的点只要在数组边界之内并且其特征与初始特征不一致，我们就将其变为与起始点同一特征（染色）。同时将这些新染色的点作为起始再向四周扩散一步，执行相同操作，直到全部同化完成。

回到本题，与之前做过的题目稍有不同的是，bfs可扩散的范围不仅包括上下左右，还要包括左上，左下，右上和右下，总共8个方向。其实，如果我们搞懂了bfs的精髓，别说8个方向，就是8百个方向解法也不会变。

首先我们将左上角作为bfs起始点，开始向8个方向扩散，考虑到边界以及阻塞（1），实际可以扩散的方向可能要小于8。我们将符合条件的方向存储下来，作为下一步bfs的起始条件，继续扩散，直到触及到右下角为止。bfs的步数再加1即是结果（注意本题求的是路径长度，加一是为了包含起始位置）。

唯一需要注意的一个坑是，如果起始位置左上角的值是1，那么可以直接返回-1。

完整代码：

public int shortestPathBinaryMatrix(int[][] grid) {
    int length = grid.length; // 矩阵边长
    if(grid[0][0]==1){ // 如果左上角为1，直接返回-1
        return -1;
    }
    if(length==1){ // 如果变长为1，返回1
        return 1;
    }
    // 定义八个方向
    int[][] directions = new int[][]{{1,0},{-1,0},{0,1},{0,-1},{-1,-1},{-1,1},{1,-1},{1,1}};
    Queue<int[]> q = new LinkedList<>(); // bfs用的Queue
    q.offer(new int[]{0,0}); // 将左上角加入queue，作为bfs起始
    boolean visited[][] = new boolean[length][length];
    visited[0][0]=true; // 左上角标记为已访问状态，防止重复访问
    int res=1; // 定义结果
    while(q.size()>0){ // 开始bfs常规操作
        int size = q.size();
        while(size>0){
            size--;
            int[] point = q.poll();
            for(int[] direciton : directions){
                int row = point[0] + direciton[0], col = point[1] + direciton[1];
                // 如果扩散的点不越界，并没有被访问过，并且值不为1，则将此点加入Queue
                if(row>=0 && row < length && col>= 0 && col<length && grid[row][col]==0 && !visited[row][col] ){
                    // 找到右下角时，返回res
                    if(row == length-1 && col == grid.length-1){
                        return res+1;
                    }
                    visited[row][col] = true;
                    q.offer(new int[]{row, col});
                }
            }
        }
        res++;
    }
    return -1;
}

本解法用时20ms。

Runtime: 20 ms, faster than 72.42% of Java online submissions for Shortest Path in Binary Matrix.

Memory Usage: 46.9 MB, less than 100.00% of Java online submissions for Shortest Path in Binary Matrix.

本网站文章均为原创内容，并可随意转载，但请标明本文链接
如有任何疑问可在文章底部留言。为了防止恶意评论，本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言，并会在第一时间对您的留言进行回复！欢迎交流！
本文链接: https://leetcode.jp/leetcode-1091-shortest-path-in-binary-matrix-解题思路分析/