LEETCODE常见算法之深度优先搜索DFS超详细白话讲解(上)

DFS是我刷题以来接触比较早的一类算法，DFS全称Deep First Search，中文名叫做深度优先搜索。单纯看名称你就会明白，该算法是为了解决搜索问题。网上介绍DFS的文章不在少数，因此本篇博客的初衷并不是为了深入探讨该算法的优缺点，而是帮助大家理解如何使用该算法来解决LEETCODE上的相关题目。

DFS核心思想

深度优先搜索的核心是递归，如果你对递归思想还不是很了解，那么你不可能完全理解dfs的本质，我们会在下文对递归做出一些简单的解释。文章开头我们提到过，dfs是解决搜索问题，那么它是解决什么类型的搜索呢？答案是路径搜索。它的使用场景通常存在以下几种：

• 遍历树结构
• 遍历图结构
• 在二维数组中遍历路径

这里说句题外话，与dfs相关的另外一种算法叫做bfs，它是广度优先搜索的缩写，这种算法我们会在之后的文章中讲到，它的使用场景与dfs非常类似，这里我们先略过不提。总之，当你在leetcode中或是面试时看到上述类型的题目时，你应该首先想到使用dfs或者是bfs来解题，快速确定一道题的解题思路，对你做题的帮助非常大。

接下来，我们使用leetcode中经典的例子来帮助大家深入理解dfs的用法。

先来一道简单题热热身。

---

例1：层数最深叶子节点的和

给你一棵二叉树，请你返回层数最深的叶子节点的和。

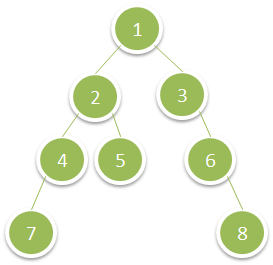
输入：root = [1,2,3,4,5,null,6,7,null,null,null,null,8]
输出：15

原题链接：

• 英文： https://leetcode.com/problems/deepest-leaves-sum/
• 中文： https://leetcode-cn.com/problems/deepest-leaves-sum/
• 题目公司信息： https://leetcode.jp/problemdetail.php?id=1302

这是一道二叉树题目，也是dfs算法经典的使用场景。当然使用bfs同样可以解题，我们会在之后的文章中做出介绍。大家首先思考一下，为什么说dfs适合于此类型的题目？还记得dfs的核心吗，是递归，递归方法解决的是重复相同子问题，对于二叉树的任意一个节点，它都有可能存在0-2个子节点，而他的子节点同样也都会存在0-2个子节点，当前问题与子问题的场景如出一辙。在我们初学编程时，大家都知道解决相同问题时可以使用循环来大幅减少代码量，比如输出一个数组arr中的所有元素：

for(int i=0;i<arr.length;i++) print(arr[i]);

那么问题来了，递归与循环的区别在哪里？区别在于路径的数目！我们看上面这个打印数组的问题，它的路径只有一条，即从头到尾，中间没有任何其他岔路。而二叉树则不同，每个节点下面都存在了0-2条岔路，使用循环，或者说使用一层循环肯定是无法做到的。对于这种路径很多又很复杂的问题，递归就是最好的解决方案。

回到本题，大家可能还有一个疑问，题目求解的是最深层叶子节点的和，这与路径有毛线关系？如果你能提出这样的疑问，说明你已经在认真思考dfs了，二叉树类题目，考官一般只会给出二叉树的根节点，要想找到某个叶子节点，你必须要从根节点一步一步向下走，直到走到某一个叶子节点为止，你走的整个过程实际上就是一条路径，并且你必须走完所有路径，才能找到所有叶子节点。

接下来，我们讨论如何遍历二叉树的所有路径。首先从根节点出发，如果它存在左侧子节点，我们继续向其左侧子节点进发（这就是递归！在这里我们称之为向下dfs）。同理，如果它存在右侧子节点，我们也可以继续向其右侧子节点进发。两个进发方向，实际上是分出了2条线路。递归到子问题后（左子节点或者右子节点），逻辑与当前逻辑完全相同，又会分叉出一些新的路径。递归的终止条件即是找到叶子节点为止，即它不存在左子节点也不存在右子节点。我们用代码来描述一下上述逻辑：

void dfs(Node node){
    // 遇到叶子节点，递归终止
    if(node.left==null&&node.right==null) return;
    // 如果存在左子节点，dfs至左子节点
    if(node.left!=null) dfs(node.left);
    // 如果存在右子节点，dfs至右子节点
    if(node.right!=null) dfs(node.right);
}

上面的代码不难理解，他就是dfs标准的模板写法。这种写法不仅可以利用在二叉树问题上，对于多叉树或是图也完全适用，只不过递归方法中不仅仅要递归2个子节点，而是要递归它所有的子节点才可以。接下来，为了更直观的看出dfs路径搜索过程，我们来模拟一下dfs的执行顺序，还是使用题目的例子：

1. 从根节点1出发，它存在左子节点，dfs至左子节点2
2. 节点2存在左子节点，dfs至左子节点4
3. 节点4存在左子节点，dfs至左子节点7
4. 7不存在子节点，为叶子节点，递归终止，返回上层递归节点4
5. 节点4不存在右子节点，返回上层递归节点2
6. 节点2存在右子节点，dfs至右子节点5
7. 5不存在子节点，为叶子节点，递归终止，返回上层递归节点2
8. 节点2左右子节点均递归结束，返回上层递归节点1
9. 节点1存在右子节点，dfs至右子节点3
10. 节点3不存在左子节点，但存在右子节点，递归至右子节点6.
11. 节点6不存在左子节点，但存在右子节点，递归至右子节点8.
12. 8不存在子节点，为叶子节点，递归终止，返回上层递归节点6
13. 节点6左右子节点均递归结束，返回上层递归节点3
14. 节点3左右子节点均递归结束，返回上层递归节点1
15. 节点1左右子节点均递归结束，递归结束

通过上述模拟过程可以看出，我们遇到任意节点时，先dfs其左侧子节点，一路向下到达最左侧叶子节点，然后返回上层递归，继续dfs其右侧节点，而该右侧节点也是优先dfs其左侧子节点，直到所有节点都遍历结束。实际解题时，dfs顺序并不重要，你也可以先dfs右侧节点，这并不影响最终的结果。

另外，上述代码中我们没有做任何实际的操作，只是遍历了所有路径而已，对于不同的题目，你可以在上述代码的框架下，加上你所需要的内容即可，比如你想知道所有叶子节点的和，这时代码可以修改为：

// 返回当前节点下方所有叶子节点的和
int dfs(Node node){
    // 遇到叶子节点，返回叶子节点的值
    if(node.left==null&&node.right==null) return node.val;
    int sum=0; // 所有叶子节点的和
    // 如果存在左子节点，dfs至左子节点，
    // 查看其左子节点下所有叶子节点的和，并累加至sum
    if(node.left!=null) sum+=dfs(node.left);
    // 如果存在右子节点，dfs至右子节点
    // 查看其右子节点下所有叶子节点的和，并累加至sum
    if(node.right!=null) sum+=dfs(node.right);
    return sum;
}

对于本题，题目要求只返回最深层叶子节点的和，那么你就需要知道最深层的层数，求最深层层数同样可以使用dfs，我们将上述方法的返回值定义为当前节点下最深层层数,另外在参数中添加一个当前层数，根节点默认层数是0：

// level为当前节点层数，根节点默认为0
// 返回当前节点下方最深层叶子节点的层数
int dfs(Node node, int level){
    // 遇到叶子节点，返回叶子节点的层数
    if(node.left==null&&node.right==null) return level;
    int max=0; // 当前节点下最深层叶子节点层数
    // 如果存在左子节点，dfs至左子节点，
    // 查看其左子节点下最深层层数
    if(node.left!=null) max=Math.max(max,dfs(node.left,level+1));
    // 如果存在右子节点，dfs至右子节点
    // 查看其右子节点下最深层层数
    if(node.right!=null) max=Math.max(max,dfs(node.right,level+1));
    return max;
}

如果你已经理解了上述代码，恭喜你已经基本上掌握了dfs的精髓，至于本题的解法我想你也有了大致的思路。本文用这道题来举例，是想让大家加深对dfs以及递归的理解，另外你想查看本题的详细解题思路，可以参照我之前的文章：

LEETCODE 1302. Deepest Leaves Sum 解题思路分析

接下来，我们会使用一道Hard级别的题目，继续探讨dfs的用法。

下文链接：LEETCODE常见算法之深度优先搜索DFS超详细白话讲解(下)

本网站文章均为原创内容，并可随意转载，但请标明本文链接
如有任何疑问可在文章底部留言。为了防止恶意评论，本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言，并会在第一时间对您的留言进行回复！欢迎交流！
本文链接: https://leetcode.jp/leetcode常见算法之深度优先搜索dfs超详细白话讲解上/