SortAlgorithm
七种基本排序算法的实现和总结。GitHub地址
https://github.com/zcbiner/SortAlgorithm
一、冒泡排序
每次比较两个相邻的元素,如果它们的顺序错误就把它们交换过来。
步骤:
比较相邻的元素。如果倒数第一个比倒数第二个小,就交换他们两个。
对第0个到第n-1个数据做同样的工作。这时,最小的数就“浮”到了数组最开始的位置上。
针对所有的元素重复以上的步骤,除了第一个。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
代码实现:
for (int i = 0; i < arr.length; i++) {
for (int j = arr.length - 1; j > i; j--) {
if (arr[j] < arr[j - 1]) {
SortUtil.swap(arr, j, j - 1);
}
}
}二、选择排序
不断地选择剩余元素中的最小者。
最大特点是交换移动数据次数相当少。
步骤:
找到数组中最小元素的下标,将第一个元素与最小元素下标的数进行交换。
在剩下的元素中找到最小元素下标并将其与数组第二个元素交换,直至整个数组排序。
代码实现:
for (int i = 0; i < arr.length; i++) {
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
SortUtil.swap(arr, minIndex, i);
}三、插入排序
插入排序的工作原理是,对于每个未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
步骤:
从第一个元素开始,该元素可以认为已经被排序
取出下一个元素,在已经排序的元素序列中从后向前扫描
如果被扫描的元素(已排序)大于新元素,将该元素后移一位
重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
将新元素插入到该位置后
重复步骤2~5
代码实现:
for (int i = 1; i < arr.length; i++) {
int temp = arr[i]; int j;
for (j = i; j > 0 && (arr[j - 1] > temp); j--) {
arr[j] = arr[j -1];
}
arr[j] = temp;
}四、归并排序
将长度为n的记录不断划分,划分到长度为1时,再两两合并,依次递归。主要是利用分治法来处理。
代码实现:
@Overridepublic int[] sort(int[] arr) {
mergeSort(arr, 0, arr.length - 1); return arr;
}private void mergeSort(int[] array, int start, int end) {
if (start >= end) return; int middle = (start + end) / 2;
mergeSort(array, start, middle);
mergeSort(array, middle + 1, end);
merge(array, start, middle, end);
}private void merge(int[] array, int start, int middle, int end) {
int[] aux = new int[end - start + 1];
System.arraycopy(array, start, aux, 0, end - start + 1);
int left = start; int right = middle + 1;
for (int k = start; k <= end; k++) {
if (left > middle) {
array[k] = aux[right - start];
right++;
} else if (right > end) {
array[k] = aux[left - start];
left++;
} else if (aux[left - start] > aux[right - start]) {
array[k] = aux[right - start];
right++;
} else { array[k] = aux[left - start];
left++;
}
}
}五、堆排序
堆排序就是利用堆进行排序的方法.基本思想是:将待排序的序列构造成一个大顶堆.此时,整个序列的最大值就是堆顶的根结点.将它移
走(其实就是将其与堆数组的末尾元素交换, 此时末尾元素就是最大值),然后将剩余的n-1个序列重新构造成一个堆,这样就会得到n个元素的次大值.如此反复执行,便能得到一个有序序列了。
步骤:
构造最大堆(Build_Max_Heap):若数组下标范围为0~n,考虑到单独一个元素是大根堆,则从下标n/2开始的元素均为大根堆。于是只要从n/2-1开始,向前依次构造大根堆,这样就能保证,构造到某个节点时,它的左右子树都已经是大根堆。
堆排序(HeapSort):由于堆是用数组模拟的。得到一个大根堆后,数组内部并不是有序的。因此需要将堆化数组有序化。思想是移除根节点,并做最大堆调整的递归运算。第一次将heap[0]与heap[n-1]交换,再对heap[0…n-2]做最大堆调整。第二次将heap[0]与heap[n-2]交换,再对heap[0…n-3]做最大堆调整。重复该操作直至heap[0]和heap[1]交换。由于每次都是将最大的数并入到后面的有序区间,故操作完后整个数组就是有序的了。
最大堆调整(Max_Heapify):该方法是提供给上述两个过程调用的。目的是将堆的末端子节点作调整,使得子节点永远小于父节点 。
代码实现:
public int[] sort(int[] arr) {
int len = arr.length - 1;
for (int i = len / 2 - 1; i >= 0; i--) {
headAdjust(arr, i, len);
} while (len >= 0) {
SortUtil.swap(arr, 0, len--);
headAdjust(arr, 0, len);
} return arr;
}private void headAdjust(int[] arr, int parent, int len) {
int leftChild, rightChild, maxChild;
while ((leftChild = 2 * parent + 1) <= len) {
rightChild = leftChild + 1;
maxChild = leftChild; // 将maxChild指向左右子节点中的较大者
if (maxChild < len && (arr[leftChild] < arr[rightChild])) {
maxChild++;
} if (arr[parent] < arr[maxChild]) {
SortUtil.swap(arr, parent, maxChild);
parent = maxChild;
} else { break;
}
}
}六、希尔排序
先将整个待排元素序列分割成若干子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序(增量为1)。其时间复杂度为O( n^3/2 ),要好于直接插入排序的O(n^2)
代码实现:
int gap = arr.length / 2;while (gap >= 1) {
for (int i = gap; i < arr.length; i++) {
int temp = arr[i];
int j = i - gap;
while (j >= 0 && arr[j] > temp) {
arr[j + gap] = arr[j];
j -= gap;
}
arr[j + gap] = temp;
}
gap /= 2;
}注:希尔排序的gap取值不仅仅是arr.length/2这么简单,可以根据数据特性选取合适的值达到最高的运行效率。
七、快速排序
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
步骤:
从数列中挑出一个元素作为基准数。
分区过程,将比基准数大的放到右边,小于或等于它的数都放到左边。
再对左右区间递归执行第二步,直至各区间只有一个数。
代码实现:
private void quickSort(int[] arr, int left, int right) {
if (left >= right) return;
int i = left, j = right, temp = arr[left];
while (i < j) {
while (i < j && arr[j] >= temp) {
j--;
} while (i < j && arr[i] <= temp) {
i++;
} if (i < j) {
SortUtil.swap(arr, i, j);
}
}
arr[left] = arr[i];
arr[i] = temp;
quickSort(arr, left, i - 1);
quickSort(arr, i + 1, right);
}八、数据测试与比较
对以上7种排序算法进行测试。测试数据由以下函数随机生成:
public static int[] randomArray(int length, int bound) {
int[] a = new int[length];
Random random = new Random();
for (int i = 0; i < length; i++) {
a[i] = random.nextInt(bound);
} return a;
}该函数有两个参数,length表示生成的数据量;bound表示数据的范围值。改变length和bound进行测试。
length=5000, bound=10000:
排序名称:冒泡排序 消耗时间:45ms 排序名称:选择排序 消耗时间:13ms 排序名称:插入排序 消耗时间:12ms 排序名称:希尔排序 消耗时间:3ms 排序名称:归并排序 消耗时间:2ms 排序名称:堆排序 消耗时间:2ms 排序名称:快速排序 消耗时间:1ms
length=10000, bound=10000:
排序名称:冒泡排序 消耗时间:197ms 排序名称:选择排序 消耗时间:64ms 排序名称:插入排序 消耗时间:27ms 排序名称:希尔排序 消耗时间:3ms 排序名称:归并排序 消耗时间:4ms 排序名称:堆排序 消耗时间:5ms 排序名称:快速排序 消耗时间:4ms
length=20000, bound=100000:
排序名称:冒泡排序 消耗时间:768ms 排序名称:选择排序 消耗时间:163ms 排序名称:插入排序 消耗时间:74ms 排序名称:希尔排序 消耗时间:5ms 排序名称:归并排序 消耗时间:4ms 排序名称:堆排序 消耗时间:4ms 排序名称:快速排序 消耗时间:5ms
以上的数据没有很大的代表性,而且测试面不全,因此只能得出大概的结论。(由于生成的是随机数据,因此每次运行时间都有细微差异)
首先看到,冒泡排序的时间消耗是最多的。因为它的比较,交换最多。
插入排序的性能优于选择排序。(可以看看知乎的评论)
总体来说,希尔、归并、堆和快速排序是比较好的选择。
九、排序算法总结
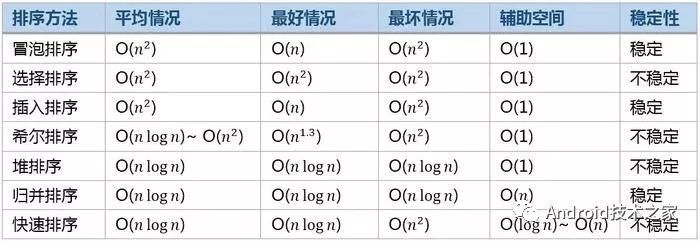
排序算法总结
喜欢 就关注吧,欢迎投稿!

作者:zcbiner
链接:https://www.jianshu.com/p/250d12096e54
來源:简书
简书著作权归作者所有,任何形式的转载都请联系作者获得授权并注明出处。
本网站文章均为原创内容,并可随意转载,但请标明本文链接
如有任何疑问可在文章底部留言。为了防止恶意评论,本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言,并会在第一时间对您的留言进行回复!欢迎交流!
本文链接: https://leetcode.jp/排序算法的实现与比较/