题目大意：
受标签影响的最大值
我们有一个项的集合，其中第 i 项的值为 values[i]，标签为 labels[i]。
我们从这些项中选出一个子集 S，这样一来：
L，子集 S 中标签为 L 的项的数目总满足 <= use_limit。 返回子集 S 的最大可能的 和。
题目大意：
二进制矩阵中的最短路径
在一个 N × N 的方形网格中，每个单元格有两种状态：空（0）或者阻塞（1）。
一条从左上角到右下角、长度为 k 的畅通路径，由满足下述条件的单元格 C_1, C_2, ..., C_k 组成：
C_i 和 C_{i+1} 在八个方向之一上连通（此时，C_i 和 C_{i+1} 不同且共享边或角）C_1 位于 (0, 0)（即，值为 grid[0][0]）C_k 位于 (N-1, N-1)（即，值为 grid[N-1][N-1]）C_i 位于 (r, c)，则 grid[r][c] 为空（即，grid[r][c] == 0）返回这条从左上角到右下角的最短畅通路径的长度。如果不存在这样的路径，返回 -1 。
题目大意：
拼车
假设你是一位顺风车司机，车上最初有 capacity 个空座位可以用来载客。由于道路的限制，车 只能 向一个方向行驶（也就是说，不允许掉头或改变方向，你可以将其想象为一个向量）。
这儿有一份行程计划表 trips[][]，其中 trips[i] = [num_passengers, start_location, end_location] 包含了你的第 i 次行程信息：
・必须接送的乘客数量；
・乘客的上车地点；
・以及乘客的下车地点。
这些给出的地点位置是从你的 初始 出发位置向前行驶到这些地点所需的距离（它们一定在你的行驶方向上）。
请你根据给出的行程计划表和车子的座位数，来判断你的车是否可以顺利完成接送所用乘客的任务（当且仅当你可以在所有给定的行程中接送所有乘客时，返回 true，否则请返回 false）。
继续阅读题目大意：
地图分析
你现在手里有一份大小为 N x N 的『地图』（网格） grid，上面的每个『区域』（单元格）都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地，你知道距离陆地区域最远的海洋区域是是哪一个吗？请返回该海洋区域到离它最近的陆地区域的距离。
我们这里说的距离是『曼哈顿距离』（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个区域之间的距离是 |x0 – x1| + |y0 – y1| 。
如果我们的地图上只有陆地或者海洋，请返回 -1。
示例 1：
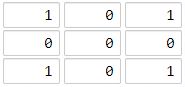
输入：[[1,0,1],[0,0,0],[1,0,1]] 输出：2 解释： 海洋区域 (1, 1) 和所有陆地区域之间的距离都达到最大，最大距离为 2。
示例 2：
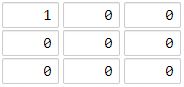
输入：[[1,0,0],[0,0,0],[0,0,0]] 输出：4 解释： 海洋区域 (2, 2) 和所有陆地区域之间的距离都达到最大，最大距离为 4。
提示：
1 <= grid.length == grid[0].length <= 100grid[i][j] 不是 0 就是 1题目大意：
在一棵无限的二叉树上，每个节点都有两个子节点，树中的节点 逐行 依次按 “之” 字形进行标记。
如下图所示，在奇数行（即，第一行、第三行、第五行……）中，按从左到右的顺序进行标记；
而偶数行（即，第二行、第四行、第六行……）中，按从右到左的顺序进行标记。
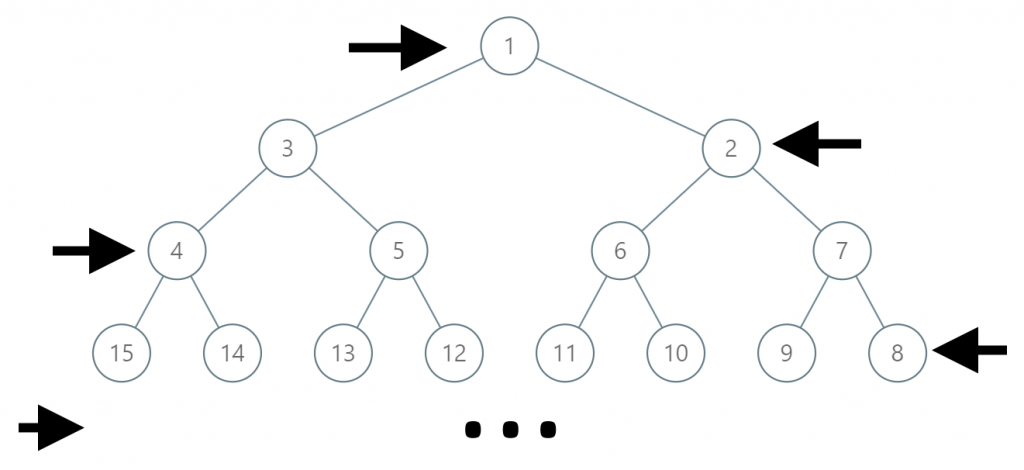
给你树上某一个节点的标号 label，请你返回从根节点到该标号为 label 节点的路径，该路径是由途经的节点标号所组成的。
示例 1：
输入：label = 14
输出：[1,3,4,14]
示例 2：
输入：label = 26
输出：[1,2,6,10,26]
提示：
1 <= label <= 10^6
继续阅读题目大意：
最大的以 1 为边界的正方形
给你一个由若干 0 和 1 组成的二维网格 grid，请你找出边界全部由 1 组成的最大 正方形 子网格，并返回该子网格中的元素数量。如果不存在，则返回 0。
示例 1：
输入：grid = [[1,1,1],[1,0,1],[1,1,1]]
输出：9
示例 2：
输入：grid = [[1,1,0,0]]
输出：1
题目大意：
交替打印FooBar
我们提供一个类：
class FooBar {
public void foo() {
for (int i = 0; i < n; i++) {
print(“foo”);
}
}
public void bar() {
for (int i = 0; i < n; i++) {
print(“bar”);
}
}
}
两个不同的线程将会共用一个 FooBar 实例。其中一个线程将会调用 foo() 方法，另一个线程将会调用 bar() 方法。
请设计修改程序，以确保 “foobar” 被输出 n 次。
继续阅读题目大意：
有效括号的嵌套深度
有效括号字符串 仅由 “(” 和 “)” 构成，并符合下述几个条件之一：
空字符串
连接，可以记作 AB（A 与 B 连接），其中 A 和 B 都是有效括号字符串
嵌套，可以记作 (A)，其中 A 是有效括号字符串
类似地，我们可以定义任意有效括号字符串 s 的 嵌套深度 depth(S)：
s 为空时，depth(“”) = 0
s 为 A 与 B 连接时，depth(A + B) = max(depth(A), depth(B))，其中 A 和 B 都是有效括号字符串
s 为嵌套情况，depth(“(” + A + “)”) = 1 + depth(A)，其中 A 是有效括号字符串
例如：””，”()()”，和 “()(()())” 都是有效括号字符串，嵌套深度分别为 0，1，2，而 “)(” 和 “(()” 都不是有效括号字符串。
给你一个有效括号字符串 seq，将其分成两个不相交的子序列 A 和 B，且 A 和 B 满足有效括号字符串的定义（注意：A.length + B.length = seq.length）。
现在，你需要从中选出 任意 一组有效括号字符串 A 和 B，使 max(depth(A), depth(B)) 的可能取值最小。
返回长度为 seq.length 答案数组 answer ，选择 A 还是 B 的编码规则是：如果 seq[i] 是 A 的一部分，那么 answer[i] = 0。否则，answer[i] = 1。即便有多个满足要求的答案存在，你也只需返回 一个。
继续阅读题目大意：
课程表 II
现在你总共有 n 门课需要选，记为 0 到 n-1。
在选修某些课程之前需要一些先修课程。 例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们: [0,1]
给定课程总量以及它们的先决条件，返回你为了学完所有课程所安排的学习顺序。
可能会有多个正确的顺序，你只要返回一种就可以了。如果不可能完成所有课程，返回一个空数组。
继续阅读题目大意：
课程表
现在你总共有 n 门课需要选，记为 0 到 n-1。
在选修某些课程之前需要一些先修课程。 例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们: [0,1]
给定课程总量以及它们的先决条件，判断是否可能完成所有课程的学习？