两个数组间的距离值
给你两个整数数组 arr1 ， arr2 和一个整数 d ，请你返回两个数组之间的 距离值 。
「距离值」 定义为符合此描述的元素数目：对于元素 arr1[i] ，不存在任何元素 arr2[j] 满足 |arr1[i]-arr2[j]| <= d 。
继续阅读如果你想了解leetcode中某道题目的解题思路，但本博客还未发布过相关的讲解文章，你可以在任意文章下留言，催促博主更新哦！（留言无需注册）
站内搜索
近期文章
标签
功能
LEETCODE 1391. Check if There is a Valid Path in a Grid 解题思路分析
题目大意：
检查网格中是否存在有效路径
给你一个 m x n 的网格 grid。网格里的每个单元都代表一条街道。grid[i][j] 的街道可以是：
- 1 表示连接左单元格和右单元格的街道。
- 2 表示连接上单元格和下单元格的街道。
- 3 表示连接左单元格和下单元格的街道。
- 4 表示连接右单元格和下单元格的街道。
- 5 表示连接左单元格和上单元格的街道。
- 6 表示连接右单元格和上单元格的街道。
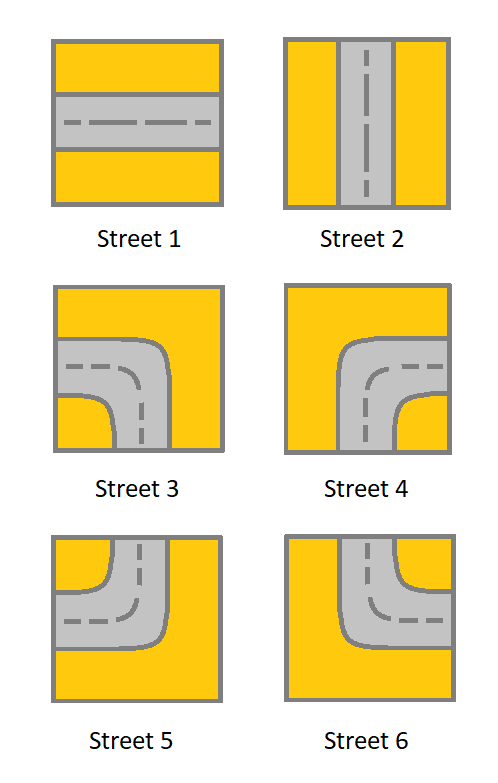
你最开始从左上角的单元格 (0,0) 开始出发，网格中的「有效路径」是指从左上方的单元格 (0,0) 开始、一直到右下方的 (m-1,n-1) 结束的路径。该路径必须只沿着街道走。
注意：你 不能 变更街道。
如果网格中存在有效的路径，则返回 true，否则返回 false 。
继续阅读LEETCODE 1386. Cinema Seat Allocation 解题思路分析
题目大意：
安排电影院座位
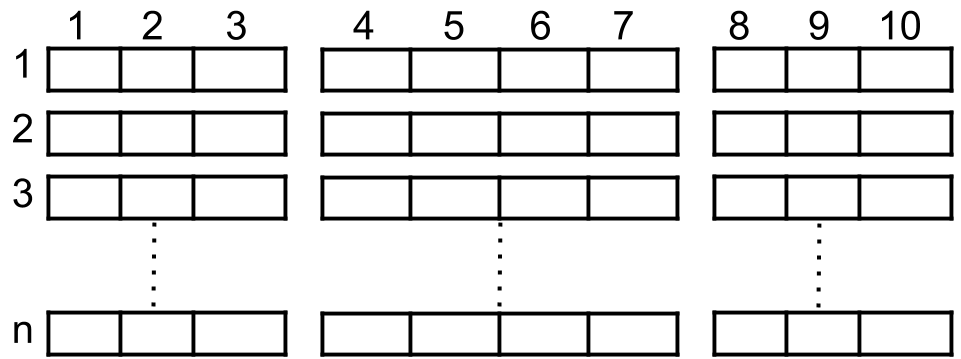
如上图所示，电影院的观影厅中有 n 行座位，行编号从 1 到 n ，且每一行内总共有 10 个座位，列编号从 1 到 10 。
给你数组 reservedSeats ，包含所有已经被预约了的座位。比如说，researvedSeats[i]=[3,8] ，它表示第 3 行第 8 个座位被预约了。
请你返回 最多能安排多少个 4 人家庭 。4 人家庭要占据 同一行内连续 的 4 个座位。隔着过道的座位（比方说 [3,3] 和 [3,4]）不是连续的座位，但是如果你可以将 4 人家庭拆成过道两边各坐 2 人，这样子是允许的。
LEETCODE 1387. Sort Integers by The Power Value 解题思路分析
题目大意：
将整数按权重排序
我们将整数 x 的 权重 定义为按照下述规则将 x 变成 1 所需要的步数：
- 如果 x 是偶数，那么 x = x / 2
- 如果 x 是奇数，那么 x = 3 * x + 1
比方说，x=3 的权重为 7 。因为 3 需要 7 步变成 1 （3 –> 10 –> 5 –> 16 –> 8 –> 4 –> 2 –> 1）。
给你三个整数 lo， hi 和 k 。你的任务是将区间 [lo, hi] 之间的整数按照它们的权重 升序排序 ，如果大于等于 2 个整数有 相同 的权重，那么按照数字自身的数值 升序排序 。
请你返回区间 [lo, hi] 之间的整数按权重排序后的第 k 个数。
注意，题目保证对于任意整数 x （lo <= x <= hi） ，它变成 1 所需要的步数是一个 32 位有符号整数。
继续阅读LEETCODE 1388. Pizza With 3n Slices 解题思路分析
题目大意：
3n 块披萨
给你一个披萨，它由 3n 块不同大小的部分组成，现在你和你的朋友们需要按照如下规则来分披萨：
- 你挑选 任意 一块披萨。
- Alice 将会挑选你所选择的披萨逆时针方向的下一块披萨。
- Bob 将会挑选你所选择的披萨顺时针方向的下一块披萨。
- 重复上述过程直到没有披萨剩下。
每一块披萨的大小按顺时针方向由循环数组 slices 表示。
请你返回你可以获得的披萨大小总和的最大值。
LEETCODE 1392. Longest Happy Prefix 解题思路分析
题目大意：
最长快乐前缀
「快乐前缀」是在原字符串中既是 非空 前缀也是后缀（不包括原字符串自身）的字符串。
给你一个字符串 s，请你返回它的 最长快乐前缀。
如果不存在满足题意的前缀，则返回一个空字符串。
LEETCODE 13. Roman to Integer 解题思路分析
题目大意：
罗马数字转整数
罗马数字包含以下七种字符: I， V， X， L，C，D 和 M。
字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M 1000
例如， 罗马数字 2 写做 II ，即为两个并列的 1。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：
I可以放在V(5) 和X(10) 的左边，来表示 4 和 9。X可以放在L(50) 和C(100) 的左边，来表示 40 和 90。C可以放在D(500) 和M(1000) 的左边，来表示 400 和 900。
给定一个罗马数字，将其转换成整数。输入确保在 1 到 3999 的范围内。
继续阅读LEETCODE 12. Integer to Roman 解题思路分析
题目大意：
整数转罗马数字
罗马数字包含以下七种字符： I， V， X， L，C，D 和 M。
字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M 1000
例如， 罗马数字 2 写做 II ，即为两个并列的 1。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：
I可以放在V(5) 和X(10) 的左边，来表示 4 和 9。X可以放在L(50) 和C(100) 的左边，来表示 40 和 90。C可以放在D(500) 和M(1000) 的左边，来表示 400 和 900。
给定一个整数，将其转为罗马数字。输入确保在 1 到 3999 的范围内。
继续阅读LEETCODE常用小知识点总结（不断更新）
一，取得十进制数字上的每一位
用当前数字与10求余数，该余数即是当前数字最低位上的数字，接下来我们将当前数字除以10，继续求它与10的余数，该数字即是次低位上的数字，重复上述过程直到当前数字为0为止。
List<Integer> list = new ArrayList<>();
// 取得x上的每一位
while(x>0){
list.add(x%10);
x/=10;
}二， 判断回文
判断一个字符串是否是回文我们通常采用剥洋葱的方式，从最外层向内比较，解题时可以定义左右两个指针，初始时左指针指向下标0，右指针指向字符串末尾位，如果当前俩指针指向的值不一致，直接返回false。反之，左指针加一，右指针减一，向内移动一层继续比较，重复此过程直到左指针不再小于右指针为止。
public boolean isPalindrome(String s) {
// 定义左右指针
int left=0,right=list.size()-1;
while(left<right){
// 左右指针指向的数字不同时，返回false
if(s.charAt(left) != s.charAt(right)){
return false;
}
left++;
right--;
}
return true;
}三，不使用额外变量交换两个数字或字符的值