题目大意:
二叉搜索树中的顺序后继
给你一个二叉搜索树和其中的某一个结点,请你找出该结点在树中顺序后继的节点。
结点 p 的后继是值比 p.val 大的结点中键值最小的结点。
示例 1:
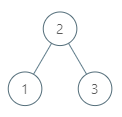
输入: root = [2,1,3], p = 1 输出: 2 解析: 这里 1 的顺序后继是 2。请注意 p 和返回值都应是 TreeNode 类型。
示例 2:
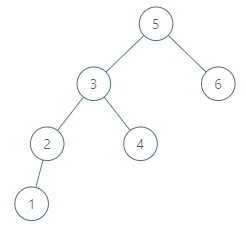
输入: root = [5,3,6,2,4,null,null,1], p = 6 输出: null 解析: 因为给出的结点没有顺序后继,所以答案就返回 null 了。
注意:
- 假如给出的结点在该树中没有顺序后继的话,请返回 null
- 我们保证树中每个结点的值是唯一的
如果想查看本题目是哪家公司的面试题,请参考以下免费链接: https://leetcode.jp/problemdetail.php?id=285
解题思路分析:
题目要找到一个节点,该节点是大于p的所有节点中最小的那个。首先考虑BST中哪些节点大于p:
- p的右子节点都大于p。
- 从节点p向上寻找根节点,如果p是该根节点的左子节点,那么该根节点大于p。
接下来,考虑所有大于p的节点中,哪个是最小的,根据上面2条结果:
- 由于p的右子树中的节点都大于p,那么右子树中最小的一定是该子树最左边的元素。
- 距离p最近的根节点,并且p是该根节点的左子树中的节点。
对于上述1和2两个节点,由于节点p和节点p的右子树都是2中描述的根节点的左子节点,所以结果2一定大于结果1,因为取所有大于p中的最小值,因此优先返回结果1,即p的右子树中最靠左的元素,如果p的右子树为空,则需要返回结果2的根节点。
实现代码:
public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
// 递归求解
return help(root,null,p.val);
}
// root:当前节点
// parent: 距离当前节点最近的根节点,并且p是该根节点左子树中的元素
// target:目标节点p的值
TreeNode help(TreeNode root, TreeNode parent, int target){
// 如果target大于当前节点,在当前节点的右子树中继续寻找
// 由于当前节点小于右子树中的值,parent不变
if(target>root.val){
return help(root.right,parent,target);
}
// 如果target小于于当前节点,在当前节点的左子树中继续寻找
// 由于当前节点大于左子树中的值,parent为当前节点
else if(target<root.val){
return help(root.left,root,target);
}
// 以下为当前节点是P的情况
// 如果右节点不为空,返回右子树中最小的元素
if(root.right!=null) return findMin(root.right);
// 如果右节点为空,返回parent
else return parent;
}
// 找到当前节点中最靠左的子节点
TreeNode findMin(TreeNode root){
if(root.left==null) return root;
return findMin(root.left);
}本题解法执行时间为2ms。
Runtime: 2 ms, faster than 100.00% of Java online submissions for Inorder Successor in BST.
Memory Usage: 46.5 MB, less than 5.26% of Java online submissions for Inorder Successor in BST.
本网站文章均为原创内容,并可随意转载,但请标明本文链接如有任何疑问可在文章底部留言。为了防止恶意评论,本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言,并会在第一时间对您的留言进行回复!欢迎交流!
本文链接: http://leetcode.jp/leetcode-285-inorder-successor-in-bst-解题思路分析/