题目大意:
T 秒后青蛙的位置
给你一棵由 n 个顶点组成的无向树,顶点编号从 1 到 n。青蛙从 顶点 1 开始起跳。规则如下:
- 在一秒内,青蛙从它所在的当前顶点跳到另一个 未访问 过的顶点(如果它们直接相连)。
- 青蛙无法跳回已经访问过的顶点。
- 如果青蛙可以跳到多个不同顶点,那么它跳到其中任意一个顶点上的机率都相同。
- 如果青蛙不能跳到任何未访问过的顶点上,那么它每次跳跃都会停留在原地。
无向树的边用数组 edges 描述,其中 edges[i] = [fromi, toi] 意味着存在一条直接连通 fromi 和 toi 两个顶点的边。
返回青蛙在 t 秒后位于目标顶点 target 上的概率。
示例 1:
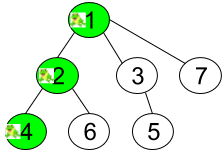
输入:n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4 输出:0.16666666666666666 解释:上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳,第 1 秒 有 1/3 的概率跳到顶点 2 ,然后第 2 秒 有 1/2 的概率跳到顶点 4,因此青蛙在 2 秒后位于顶点 4 的概率是 1/3 * 1/2 = 1/6 = 0.16666666666666666 。
示例 2:

输入:n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7 输出:0.3333333333333333 解释:上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳,有 1/3 = 0.3333333333333333 的概率能够 1 秒 后跳到顶点 7 。
示例 3:
输入:n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 20, target = 6 输出:0.16666666666666666
提示:
- 1 <= n <= 100
- edges.length == n-1
- edges[i].length == 2
- 1 <= edges[i][0], edges[i][1] <= n
- 1 <= t <= 50
- 1 <= target <= n
- 与准确值误差在 10^-5 之内的结果将被判定为正确。
如果想查看本题目是哪家公司的面试题,请参考以下免费链接: https://leetcode.jp/problemdetail.php?id=1377
解题思路分析:
这是一道有关多叉树的题目。我们需要先对数据进行预处理操作,利用所有的边构建出树形结构。树形结构我们使用Map来存储边信息。key为节点,value为该节点可以连接的其他节点列表。
接下来我们先分析第一个问题,第T秒之后青蛙正好在指定位置上的可能性:
- 第T秒时,青蛙刚好跳到target位置。
- 在未达到第T秒时,青蛙跳到了target位置,并且该位置没有与它相连的其他节点的情况下,青蛙只能target位置原地不动,当时间到达第T秒时,青蛙依然在target位置。
最后再来考虑概率。首先明确一点,由于题目给出的是树形结构,因此从起点到target的路径只存在一条。青蛙每跳一步,都是在树的岔口处做选择,跳向任意一个岔口的概率都是岔口数量分之一,我们将起点到target为止经过的所有岔口选择的概率相乘,即是最终的概率。另外需要注意一点,除了根节点之外,任意一个节点的n条边中,都会存在1条前一节点跳向当前节点的路径,由于不能跳向已访问过的节点,因此n条边中可供选择的路径实际上只有n-1条。而根节点是起始节点,所有与它连接的路径均可选择。
实现代码:
Map<Integer,List<Integer>> map = new HashMap<>();// 树形结构
double result; // 返回结果
public double frogPosition(int n, int[][] edges, int t, int target) {
// 构建树结构
for(int[] e : edges){
List<Integer> l1=map.getOrDefault(e[0],new ArrayList<>());
l1.add(e[1]);
map.put(e[0],l1);
List<Integer> l2=map.getOrDefault(e[1],new ArrayList<>());
l2.add(e[0]);
map.put(e[1],l2);
}
// dfs求解
dfs(1,1,t,target,1d);
return result;
}
// current:当前节点
// previous:前节点
// target:目标位置
// res:走到当前点的概率
void dfs(int current,int previous,int t,int target, double res){
// 与当前节点相连的其他点列表
List<Integer> list = map.get(current);
// 下一步的选择数
int count=0;
// 如果当前是根节点,下一步的选择数为list中元素个数
// 如果不是根节点,下一步的选择数为list中元素个数减一。(不能走回头路)
if(list!=null) count=current==1?list.size():list.size()-1;
// 如果当前点是目标位置
if(current==target){
// 如果当前时间是第t秒
// 或者当前位置没有其他前进路线时
// 将当前概率赋值到返回结果
if(t==0||count==0) result = res;
return;
}
// 如果已经到了第t秒,或者已经找到结果,返回
if(t==0||result>0) return;
// 当前概率变为前概率除以当前可供选择数
res=res/count;
// 循环每一条前进路线
for(int next : list){
// 如果该路线不是回头路
if(next!=previous){
// dfs到下一个节点
dfs(next,current,t-1,target,res);
}
}
}本题解法执行时间为3ms。
Runtime: 3 ms, faster than 92.48% of Java online submissions for Frog Position After T Seconds.
Memory Usage: 41 MB, less than 100.00% of Java online submissions for Frog Position After T Seconds.
本网站文章均为原创内容,并可随意转载,但请标明本文链接如有任何疑问可在文章底部留言。为了防止恶意评论,本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言,并会在第一时间对您的留言进行回复!欢迎交流!
本文链接: http://leetcode.jp/leetcode-1377-frog-position-after-t-seconds-解题思路分析/