题目大意:
分裂二叉树的最大乘积
给你一棵二叉树,它的根为 root 。请你删除 1 条边,使二叉树分裂成两棵子树,且它们子树和的乘积尽可能大。
由于答案可能会很大,请你将结果对 10^9 + 7 取模后再返回。
示例 1:
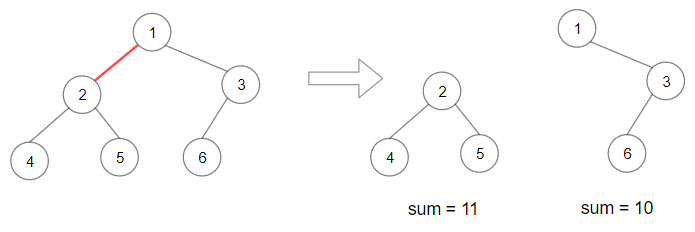
输入:root = [1,2,3,4,5,6] 输出:110 解释:删除红色的边,得到 2 棵子树,和分别为 11 和 10 。它们的乘积是 110 (11*10)
示例 2:
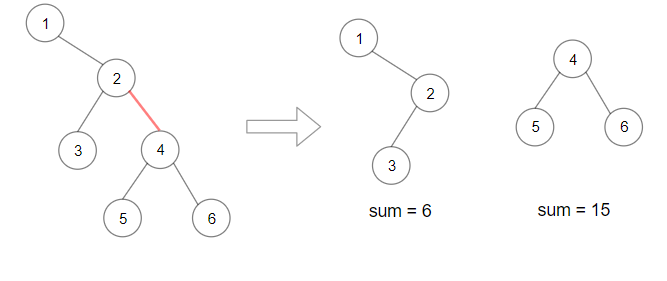
输入:root = [1,null,2,3,4,null,null,5,6] 输出:90 解释:移除红色的边,得到 2 棵子树,和分别是 15 和 6 。它们的乘积为 90 (15*6)
示例 3:
输入:root = [2,3,9,10,7,8,6,5,4,11,1] 输出:1025
示例 4:
输入:root = [1,1] 输出:1
提示:
- 每棵树最多有
50000个节点,且至少有2个节点。 - 每个节点的值在
[1, 10000]之间。
如果想查看本题目是哪家公司的面试题,请参考以下免费链接: https://leetcode.jp/problemdetail.php?id=1339
解题思路分析:
本题我们需要考虑每一种分割方式,然后在所有分割中找到一个最大乘积。解题时,我们先求出所有节点的和allSum。然后再遍历二叉树中的每一个节点,以该节点作为分割后一棵子树的根节点,求出该根节点下方所有节点的和sum,同时,分割后另外一个子树的和应该是allSum-sum。利用两棵树和的乘积更新全局最大值即可。
实现代码:
long res=0; // 返回结果
long allSum=0; // 所有节点的和
public int maxProduct(TreeNode root) {
// 先求出所有节点的和
allSum=sum(root);
// 遍历二叉树中每一个节点,以该节点作为分割后一个子树的根节点
// 并求出该子树所有节点和
sum(root);
// 返回所有分割方式中的最大乘积
return (int)(res%1000000007);
}
// 求某个节点下所有节点的和
long sum(TreeNode root){
// 如果当前节点为空,返回0
if(root==null) return 0;
// 将当前节点的值加入到和
long sum=root.val;
// 加上左子树所有节点和
sum+=sum(root.left);
// 加上右子树所有节点和
sum+=sum(root.right);
// 当前分割方式的乘积时当前根节点下子树的和乘以另外一颗子树的和
// 利用当前乘积更新全局最大值
res=Math.max(res, sum*(allSum-sum));
// 返回当前节点下所有节点和
return sum;
}本题解法执行时间为9ms。
Runtime: 9 ms, faster than 79.31% of Java online submissions for Maximum Product of Splitted Binary Tree.
Memory Usage: 57.1 MB, less than 100.00% of Java online submissions for Maximum Product of Splitted Binary Tree.
本网站文章均为原创内容,并可随意转载,但请标明本文链接如有任何疑问可在文章底部留言。为了防止恶意评论,本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言,并会在第一时间对您的留言进行回复!欢迎交流!
本文链接: http://leetcode.jp/leetcode-1339-maximum-product-of-splitted-binary-tree-解题思路分析/