题目大意:
工作计划的最低难度
你需要制定一份 d 天的工作计划表。工作之间存在依赖,要想执行第 i 项工作,你必须完成全部 j 项工作( 0 <= j < i)。
你每天 至少 需要完成一项任务。工作计划的总难度是这 d 天每一天的难度之和,而一天的工作难度是当天应该完成工作的最大难度。
给你一个整数数组 jobDifficulty 和一个整数 d,分别代表工作难度和需要计划的天数。第 i 项工作的难度是 jobDifficulty[i]。
返回整个工作计划的 最小难度 。如果无法制定工作计划,则返回 -1 。
示例 1:
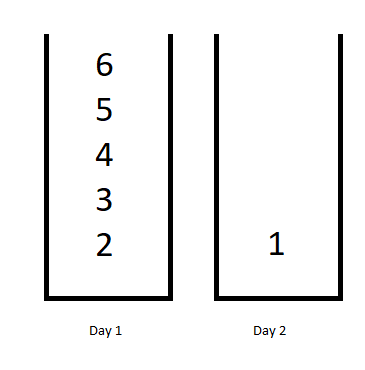
输入:jobDifficulty = [6,5,4,3,2,1], d = 2 输出:7 解释:第一天,您可以完成前 5 项工作,总难度 = 6. 第二天,您可以完成最后一项工作,总难度 = 1. 计划表的难度 = 6 + 1 = 7
示例 2:
输入:jobDifficulty = [9,9,9], d = 4 输出:-1 解释:就算你每天完成一项工作,仍然有一天是空闲的,你无法制定一份能够满足既定工作时间的计划表。
示例 3:
输入:jobDifficulty = [1,1,1], d = 3 输出:3 解释:工作计划为每天一项工作,总难度为 3 。
示例 4:
输入:jobDifficulty = [7,1,7,1,7,1], d = 3 输出:15
示例 5:
输入:jobDifficulty = [11,111,22,222,33,333,44,444], d = 6 输出:843
提示:
- 1 <= jobDifficulty.length <= 300
- 0 <= jobDifficulty[i] <= 1000
- 1 <= d <= 10
如果想查看本题目是哪家公司的面试题,请参考以下免费链接: https://leetcode.jp/problemdetail.php?id=1335
解题思路分析:
将本题的题意简单翻译一下,可以理解为,我们有一个数组,设法将数组分割成d个子数组,每个子数组中的最大值相加得到一个数值max,求所有分组情况中最小的max值。
如果之前经常看我的文章,大家应该想到,对于这种题型,我们无法判明如何分组是最优解的情况下,只能尝试遍历每一种分组情况,然后找到其中的最优解。这种思路即是动态规划思想,之前的文章我也多次提到过,对于动态规划DP类题目,可以使用递归加记忆数组的方式来求解,个人认为递归思路更加便于理解。
首先我们考虑,如果数组的个数小于d,那么无论如何我们也不能将数组分成d份,此时应该返回-1,这是本题唯一一个例外情况。除此之外,我们可以从数组的首元素开始分组,对于第一组子数组,开始位置的下标应该是0,结束下标的位置虽然不能确定,但是我们可以知道它的取值范围,即[0, length-d]之间。结束位置是0很好理解,即首元素自己是一个分组。结束位置的最大取值是数组长度减去d,这是为了保证,剩下的元素还能再分d-1组。
递归函数helper()中需要2个参数,一个是当前区间的起始下标start,另一个是剩余尚未分组的个数d,递归函数中,我们循环结束下标end的取值范围,即start至length-d之间。利用end坐标我们可以将数组分隔成为[start, end]和[end+1, 数组末尾]两部分。其中start到end区间为当前区间,当前区间的最大值为区间难度值max,而end+1到数组末尾部分的分组交给子问题去解决,递归到子问题时,区间起始下标为end加一,剩余尚未分组个数d减一。对于当前区间的每一种长度,都能计算出相应的最终结果,即:
// end>=start && end<=length-d help(start,d)=min(当前区间最大值max+help(当前区间结束坐标end+1,d-1));
循环end的每一种取值,套用上述公式,得到的所有结果中的最小值即是当前递归函数的返回值。
实现代码:
int[][] memo; // 记忆数组
public int minDifficulty(int[] jobDifficulty, int d) {
// 如果d大于数组元素个数,无法分组,返回-1
if(d>jobDifficulty.length) return -1;
// 初始化记忆数组
memo=new int[d+1][jobDifficulty.length];
// 递归求解
return help(jobDifficulty,d,0);
}
// jobDifficulty:原始数组
// d:剩余尚未分组个数
// job:当前开始job下标
// 返回值:将下标job开始到数组结尾区间分成d组,得到的最小难度值
int help(int[] jobDifficulty, int d, int job){
// 如果记忆数组中存在该值,直接返回
if(memo[d][job]>0) return memo[d][job];
// 当前区间内最大值
int maxDifficult=0;
// 返回结果
int res=Integer.MAX_VALUE;
// 当前区间最大结束坐标
int end=jobDifficulty.length-d;
// 循环每一个结束坐标
for(int i=job;i<=end;i++){
// 更新当前区间内最大值
maxDifficult=Math.max(maxDifficult, jobDifficulty[i]);
// 如果所剩分组个数大于1,继续递归分组
if(d>1){
// 当前区间最大值加上子问题的结果,为当前解,
// 利用当前解更新最优解
res=Math.min(res, maxDifficult+help(jobDifficulty,d-1,i+1));
}
}
// 如果尚未分组个数为1,返回当前区间内最大值
if(d==1) res=maxDifficult;
// 将当前最优解保存至记忆数组
memo[d][job]=res;
return res;
}本题解法执行时间为8ms。
Runtime: 8 ms, faster than 94.78% of Java online submissions for Minimum Difficulty of a Job Schedule.
Memory Usage: 37.3 MB, less than 100.00% of Java online submissions for Minimum Difficulty of a Job Schedule.
本网站文章均为原创内容,并可随意转载,但请标明本文链接如有任何疑问可在文章底部留言。为了防止恶意评论,本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言,并会在第一时间对您的留言进行回复!欢迎交流!
本文链接: http://leetcode.jp/leetcode-1335-minimum-difficulty-of-a-job-schedule-解题思路分析/