LEETCODE 1326. Minimum Number of Taps to Open to Water a Garden 解题思路分析

题目大意：

灌溉花园的最少水龙头数目

在 x 轴上有一个一维的花园。花园长度为 n，从点 0 开始，到点 n 结束。

花园里总共有 n + 1 个水龙头，分别位于 [0, 1, …, n] 。

给你一个整数 n 和一个长度为 n + 1 的整数数组 ranges ，其中 ranges[i] （下标从 0 开始）表示：如果打开点 i 处的水龙头，可以灌溉的区域为 [i –  ranges[i], i + ranges[i]] 。

请你返回可以灌溉整个花园的 最少水龙头数目 。如果花园始终存在无法灌溉到的地方，请你返回 -1 。

示例 1：

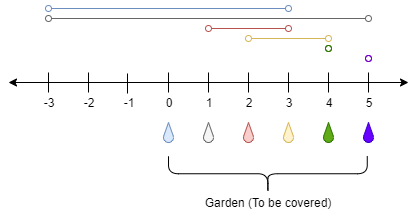
输入：n = 5, ranges = [3,4,1,1,0,0]
输出：1
解释：
 点 0 处的水龙头可以灌溉区间 [-3,3]
 点 1 处的水龙头可以灌溉区间 [-3,5]
 点 2 处的水龙头可以灌溉区间 [1,3]
 点 3 处的水龙头可以灌溉区间 [2,4]
 点 4 处的水龙头可以灌溉区间 [4,4]
 点 5 处的水龙头可以灌溉区间 [5,5]
 只需要打开点 1 处的水龙头即可灌溉整个花园 [0,5] 。

示例 2：

输入：n = 3, ranges = [0,0,0,0]
输出：-1
解释：即使打开所有水龙头，你也无法灌溉整个花园。

示例 3：

输入：n = 7, ranges = [1,2,1,0,2,1,0,1]
输出：3

示例 4：

输入：n = 8, ranges = [4,0,0,0,0,0,0,0,4]
输出：2

示例 5：

输入：n = 8, ranges = [4,0,0,0,4,0,0,0,4]
输出：1

提示：

• 1 <= n <= 10^4
• ranges.length == n + 1
• 0 <= ranges[i] <= 100

---

如果想查看本题目是哪家公司的面试题，请参考以下免费链接： https://leetcode.jp/problemdetail.php?id=1326

解题思路分析：

本题一开始想到的是使用递归思路，首层递归，循环整个花园从左至右所有的喷头，当前喷头的覆盖范围需要一个cost，当前喷头范围左边界到当前递归总范围的左边，以及当前喷头范围的右边界到当前递归总范围的右边，递归到子问题求解。两个子问题的解加一即是当前解，循环所有喷头后计算一个最小解即是当前递归的最优解。

然而提交后发现这种解法效率很低，处于TLE的边缘。于是想到了下面这种贪心算法。

首先我们算出每个喷头的范围left和right，如果left小于0，记为0，如果right大于n，记为n。我们将每个范围看作是一个线段或者区间，将区间存入一个数组maxRange[]，数组下标为该区间的left，该下标的值为区间的right。循环时，如果遇到相同left下标的值已经存在于maxRange[left]时，更新最大值存入，即代表始于当前left的区间，最远能够达到right位置。

这时问题就变的简单了，我们只需要在一堆线段中，找出最少能覆盖整个区域的线段数即可。从left为0开始找，此时maxRange[0]代表0开始的线段最远能到达的index。接下来，我们需要在[left+1, maxRange[left]]范围内一条能够到达的最远的线段即可，如果该最远线段小于等于当前maxRange[left]，说明与当前相交的所有线段中没有能够超越maxRange[left]点的线段了，因此返回-1。反之继续向后寻找，直到找到某条线段能到达终点为止。

实现代码：

public int minTaps(int n, int[] ranges) {
    // 所有喷头覆盖的区间
    int[] maxRanges = new int[n+1];
    // 循环每一个喷头
    for(int i=0;i<ranges.length;i++){
        // 喷头覆盖区间的左下标
        int left=i-ranges[i];
        // 左下标小于0时，设为0
        if(left<0) left=0;
        // 喷头覆盖区间的右下标
        int right=i+ranges[i];
        // 右下标大于n时，设为n
        if(right>n) right=n;
        // 将区间存入maxRanges
        // maxRanges[left]代表左下标为left的区间最远可以到达的坐标
        maxRanges[left] =Math.max(maxRanges[left], right);
    }
    // 找出能够覆盖整个区间的最少区间个数
    // 第一个区间从0开始，maxRanges[0]结束
    int l=0,r=maxRanges[0];
    int res=1; // 返回结果
    // 当右区间小于n时循环
    while(r<n){
        // 找到下一个区间，下一个区间的left在当前区间内
        // 并且下一个区间的right大于当前区间right
        // 找到符合上述要求的一个right最大区间
        int maxRight=r;
        int maxLeft=l;
        for(int i=l;i<=r;i++){
            if(maxRanges[i]>maxRight){
                maxRight=maxRanges[i];
                maxLeft=i;
            }
        }
        // 如果最大right不能大于当前right，返回-1
        if(maxRight==r) return -1;
        // 更新下一个区间的left和right
        r=maxRight;
        l=maxLeft+1;
        res++;
    }
    return res;
}

本题解法执行时间为2ms。

Runtime: 3 ms, faster than 100.00% of Java online submissions for Minimum Number of Taps to Open to Water a Garden.

Memory Usage: 47.2 MB, less than 100.00% of Java online submissions for Minimum Number of Taps to Open to Water a Garden.

本网站文章均为原创内容，并可随意转载，但请标明本文链接
如有任何疑问可在文章底部留言。为了防止恶意评论，本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言，并会在第一时间对您的留言进行回复！欢迎交流！
本文链接: http://leetcode.jp/leetcode-1326-minimum-number-of-taps-to-open-to-water-a-garden-解题思路分析/