LEETCODE 1183. Maximum Number of Ones 解题思路分析

题目大意：

矩阵中 1 的最大数量

有一个宽为width，高位height的矩阵M，其中每个格子的数值不是0就是1，另外矩阵M所有大小为 sideLength * sideLength 的子矩阵中，数字1的个数不能超过maxOnes。

求矩阵M中最多可以包含多少个1。

示例1：

输入: width = 3, height = 3, sideLength = 2, maxOnes = 1
输出: 4
解释:
In a 3*3 matrix, no 2*2 sub-matrix can have more than 1 one.
The best solution that has 4 ones is:
[1,0,1]
[0,0,0]
[1,0,1]

示例2：

输入: width = 3, height = 3, sideLength = 2, maxOnes = 2
输出: 6
解释:
[1,0,1]
[1,0,1]
[1,0,1]

提示：

• 1 <= width, height <= 100
• 1 <= sideLength <= width, height
• 0 <= maxOnes <= sideLength * sideLength

---

如果想查看本题目是哪家公司的面试题，请参考以下免费链接： https://leetcode.jp/problemdetail.php?id=1183

解题思路分析：

这道题要想到一个贪心思想，如果要保证全局矩阵中1的数量最多，那么，我们可以将矩阵以sideLength * sideLength分割成N个部分（矩阵边缘会存在不完全子矩阵），其中每个部分中1所在的相对位置要保持一致。比如像下面这个样子：

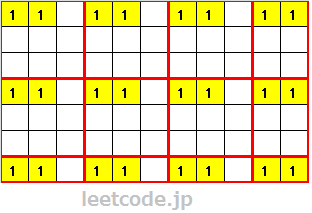
上图为11*7的矩阵，子矩阵为3*3，每个子矩阵中最多含有2个1。我们可以将子矩阵看做是一个框，无论我们将这个框放在整个矩阵的任何位置上，都能保证框内不会超过2个1。比如：

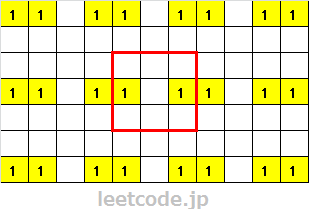
证明这个结论也不难，因为所有格子都是复制出来的，无论我们如何移动红框，移出的部分一定等于移入的部分，因此1的数量也不会改变。

接下来我们需要做的就是计算出如何在子矩阵里摆放 maxOnes 个1可以使得全局1的数量最多，我们可以分别循环子矩阵中每个点，查看该点对应的其他每个子矩阵上的影射点是否在整个矩阵的范围内。

通过下图看的会更加直接一些：

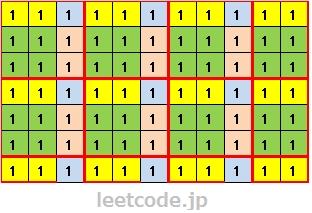
一个11*7的矩阵，我们使用3*3的子矩阵对其进行分割（红色边框），分割后，存在6个完整的3*3子矩阵，以及2个2*3子矩阵，3个3*1子矩阵，和1个2*1子矩阵。如果在黄色区域标记1，相应的我们可以得到4*3=12个1。绿色区域则是4*2=8个1，蓝色区域为3*3=9个1，粉色区域为3*2=6个1。 最后我们统计能被影射出来最多的前 maxOnes 个的和即是结果。

实现代码：

public int maximumNumberOfOnes(int width, int height, int sideLength, int maxOnes) {
    int xCount = width / sideLength; // 水平方向能够分割出多少完整子矩阵
    int yCount = height / sideLength; // 垂直方向能够分割出多少完整子矩阵
    int xRest = width % sideLength; // 水平方向剩余格子
    int yRest = height % sideLength; // 垂直方向剩余格子
    // 统计每个格子放1后，相应的可以出现多少个1
    int[] arr = new int[sideLength*sideLength];
    // 循环左上角的子矩阵中每个点
    for(int i=0;i<sideLength;i++){
        for(int j=0;j<sideLength;j++){
            if(i<xRest && j<yRest){
                // 对应上图中黄色格子
                arr[i*sideLength+j]=(xCount+1) * (yCount+1);
            }else if(i<xRest){
                // 对应上图中绿色格子
                arr[i*sideLength+j]=(xCount+1) * (yCount);
            }else if(j < yRest){
                // 对应上图中蓝色格子
                arr[i*sideLength+j]=(xCount) * (yCount+1);
            }else{
                // 对应上图中粉色格子
                arr[i*sideLength+j]=(xCount) * (yCount);
            }
        }
    }
    // 排序数组
    Arrays.sort(arr);
    int res=0;
    // 计算得出数组中前maxOnes大的和即为结果
    for(int i=arr.length-1;i>=arr.length-maxOnes;i--){
        res+=arr[i];
    }
    return res;
}

本题解法执行时间为4ms。

Runtime: 4 ms, faster than 78.92% of Java online submissions for Maximum Number of Ones.

Memory Usage: 33.6 MB, less than 100.00% of Java online submissions for Maximum Number of Ones.

本网站文章均为原创内容，并可随意转载，但请标明本文链接
如有任何疑问可在文章底部留言。为了防止恶意评论，本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言，并会在第一时间对您的留言进行回复！欢迎交流！
本文链接: http://leetcode.jp/leetcode-1183-maximum-number-of-ones-解题思路分析/