LEETCODE 1162. As Far from Land as Possible 解题思路分析

题目大意：

地图分析

你现在手里有一份大小为 N x N 的『地图』（网格） grid，上面的每个『区域』（单元格）都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地，你知道距离陆地区域最远的海洋区域是是哪一个吗？请返回该海洋区域到离它最近的陆地区域的距离。

我们这里说的距离是『曼哈顿距离』（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个区域之间的距离是 |x0 – x1| + |y0 – y1| 。

如果我们的地图上只有陆地或者海洋，请返回 -1。

示例 1：

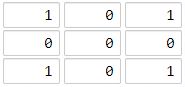
输入：[[1,0,1],[0,0,0],[1,0,1]]
输出：2
解释： 
海洋区域 (1, 1) 和所有陆地区域之间的距离都达到最大，最大距离为 2。

示例 2：

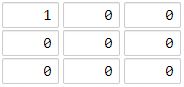
输入：[[1,0,0],[0,0,0],[0,0,0]]
输出：4
解释： 
海洋区域 (2, 2) 和所有陆地区域之间的距离都达到最大，最大距离为 4。

提示：

1. 1 <= grid.length == grid[0].length <= 100
2. grid[i][j] 不是 0 就是 1

如果想查看本题目是哪家公司的面试题，请参考以下免费链接： https://leetcode.jp/problemdetail.php?id=1162

解题思路分析：

这道题难度不大。一道简单的bfs题目。leetcode中海洋陆地问题的题目很多，大多都是bfs或是dfs题目。之前的文章已经讲过很多。这里再简单啰嗦一下bfs的思路。首先我们选取一些特征一致的点作为起始目标，然后从这些目标开始向四周扩散一步，四周的点只要在数组边界之内并且其特征与初始特征不一致，我们就将其变为与起始点同一特征（染色）。同时将这些新染色的点作为起始再向四周扩散一步，执行相同操作，直到全部同化完成。

回到本题，题目要求很明确，求离陆地最远的海洋距离。思路大致如下：

1. 先找出所有陆地的坐标，作为bfs的起始条件。
2. 通过所有的陆地坐标向外bfs。直到找到最后一块海洋为止。这期间所用到的步数即是答案。

完整代码：

public int maxDistance(int[][] grid) {
    Queue<int[]> q = new LinkedList<>();
    // 找到所有陆地坐标，将其存入bfs的Queue中
    for(int i=0;i<grid.length;i++){
        for(int j=0;j<grid[i].length;j++){
            if(grid[i][j]==1){
                q.offer(new int[]{j,i});
            }
        }
    }
    if(q.size()==0 || q.size()==grid.length * grid[0].length){
        return -1; // 如果没有陆地或者全是陆地，直接返回-1
    }
    // 开始常规bfs操作
    int count=0; // 步数，即结果（距离）
    int[][] positions = {{1,0},{-1,0},{0,1},{0,-1}};  // 定义扩散的四个方向
    while(q.size()>0){
        int size = q.size();
        while(size>0){
            size--;
            int[] land = q.poll();
            for(int[] position:positions){
                int x=land[0]+position[0],y=land[1]+position[1];
                if(x>=0 && x<grid[0].length && y>=0 && y<grid.length && grid[y][x] !=1){
                    grid[y][x] =1;
                    q.offer(new int[]{x,y});
                }
            }
        }
        count++;
    }
    return count-1;
}

本解用时17ms。

Runtime: 17 ms, faster than 86.12% of Java online submissions for As Far from Land as Possible.

Memory Usage: 47.7 MB, less than 100.00% of Java online submissions for As Far from Land as Possible.

本网站文章均为原创内容，并可随意转载，但请标明本文链接
如有任何疑问可在文章底部留言。为了防止恶意评论，本博客现已开启留言审核功能。但是博主会在后台第一时间看到您的留言，并会在第一时间对您的留言进行回复！欢迎交流！
本文链接: http://leetcode.jp/leetcode-1162-as-far-from-land-as-possible-解题思路分析/